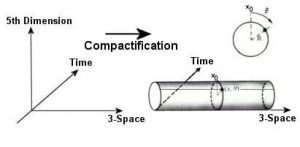
En 1921, le physicien Theodor Kaluza propose une théorie décrivant la relativité générale dans un espace-temps à 5 dimensions (1). Quelques années plus tard, en 1926, le physicien Oskar Klein démontre que cette dimension spatiale supplémentaire est extrêmement petite et enroulée sur elle-même via un mécanisme de compactification (2).
Aujourd’hui, les théories de Kaluza-Klein désignent toutes théories décrivant un espace-temps à plus de 4 dimensions. Avec l’avènement de la théorie des cordes, les modèles théoriques de type Kaluza-Klein se sont développés et sont toujours actuellement un domaine de recherche très actif en cosmologie théorique. Ainsi, par exemple, la théorie M, théorie visant à unifier les cinq types de théories des supercordes, décrit un espace-temps à 11 dimensions (7 dimensions supplémentaires).
Les écueils de la cosmologie branaire
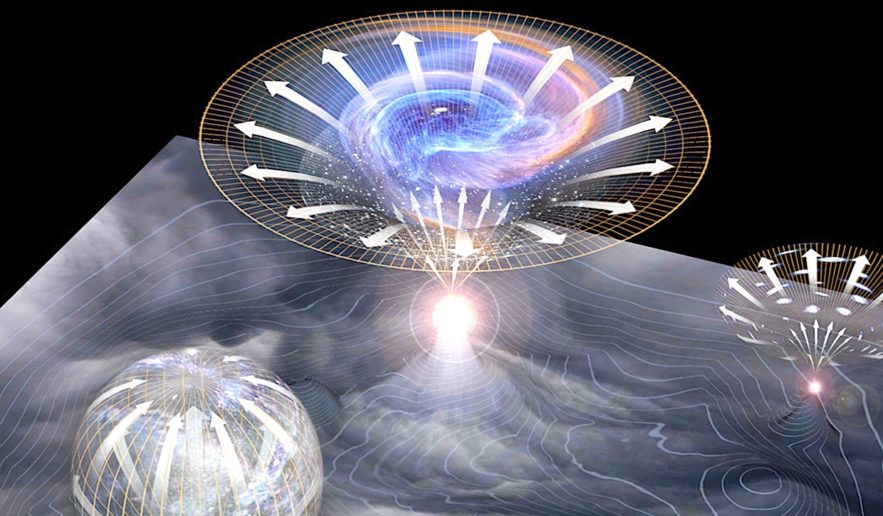
De tels modèles sont rigoureusement étudiés car la présence de dimensions supplémentaires produit nécessairement des conséquences sur l’évolution de l’univers. De nombreux modèles ont ainsi été développées dans le cadre de la cosmologie branaire propre à la théorie des cordes. Ces modèles postulent que notre univers à 4 dimensions serait contenu dans une brane elle-même contenue dans un univers extra-dimensionnel appelé « bulk ». Un exemple type est donné par le modèle d’univers ekpyrotique (voir L’univers est-il issu d’une collision branaire ?).
Dans les théories branaires, la gravité est la seule interaction élémentaire à pouvoir se propager dans toutes les dimensions, connectant les champs du Modèle Standard aux champs externes du bulk (3). Tandis que les trois autres interactions élémentaires du Modèle Standard sont prisonnières de la brane et ne peuvent se propager que dans les 3+1 dimensions visibles.

En outre, l’évolution de l’univers est notablement impactée par plusieurs facteurs. En premier lieu, la brane influe sur la densité du contenu matériel de l’univers dans la phase primitive de son évolution, lors des premiers instants suivant le Big Bang. En second lieu, le bulk interagit avec le champ gravitationnel de la brane via une « interaction sombre » (4), amenant l’univers à se comporter conformément au modèle cosmologique standard que bien plus tard dans son évolution (5).
Cependant, ces diverses conséquences ne correspondent pas aux prédictions faites par le Modèle Standard de la cosmologie, concernant les premiers instants de l’univers. En outre, les observations astrophysiques menées ces dernières années n’ont toujours pas mis en évidence les signatures cosmologiques attendues. Toutefois, un modèle alternatif correspond avec plus de cohérence au modèle cosmologique standard : le modèle des dimensions supplémentaires universelles.
Une alternative à la cosmologie branaire : les dimensions supplémentaires universelles
Dans le modèle des dimensions supplémentaires universelles
(DSU), tous les champs quantiques (bosons et fermions) peuvent se propager dans
les dimensions supplémentaires (6). Ces dernières contiennent
également leur propre type de particules appelées « partenaires de
Kaluza-Klein » et
plus massives que les particules connues du Modèle Standard
(7).
Ces particules constituent, dans le cadre des DSU, l’équivalent des superpartenaires, c’est-à-dire les particules associées aux particules du Modèle Standard dans les théories supersymétriques. La supersymétrie prédit l’existence des particules supersymétriques légères (LSPs en anglais) qui sont les particules les moins massives de toutes les particules supersymétriques.
La majorité des théories supersymétriques conservent la parité R, cela signifie que les LSPs sont des particules très stables et qu’elles ne se désintègrent pas en particules du Modèle Standard. Les LSPs neutres électriquement font ainsi d’excellents candidats à la matière noire dans les catégories des WIMPs (Weakly Interacting Massive Particles), parmi lesquels le neutralino et le gravitino (8).
De la même manière, le modèle des DSU prévoit l’existence de particules de Kaluza-Klein légères (LKPs en anglais), possédant les mêmes caractéristiques que les LSPs. Du fait de leur grande stabilité, les LKPs font, au même titre que les LSPs, de très bons candidats à la matière noire. Depuis quelques années, la liste des WIMPs s’est donc enrichie de l’hypothèse des LSPs (9).
La cohérence du modèle des DSU avec l’évolution cosmologique de l’univers
Dans une étude publiée sur arXiv le 7 novembre 2017 (10), une équipe de physiciens grecs propose un cadre théorique dans lequel le modèle des dimensions supplémentaires universelles reproduit l’évolution cosmologique de l’univers décrite par le modèle ΛCDM (le modèle cosmologique standard). Pour ce faire, le modèle des DSU doit respecter certains pré-requis.
En effet, pour obtenir un modèle cosmologique viable, le modèle proposé par les auteurs doit reproduire les résultats obtenus avec la cosmologie standard et confirmés par l’observation. Cela implique notamment de conserver les étapes importantes de l’évolution primitive de l’univers au nombre desquelles la nucléosynthèse primordiale. Tout en prenant en compte le fait que les dimensions supplémentaires n’ont toujours pas été mises expérimentalement en évidence.
De telles conditions s’imposent car la dynamique interne des dimensions supplémentaires influe nécessairement sur les constantes fondamentales de l’univers et donc sur son évolution. Or, il existe d’importantes contraintes cosmologiques sur l’amplitude de variation des constantes fondamentales ; en d’autres termes, les constantes fondamentales doivent rester constantes, et non être amenées à varier (11).
Dans le but d’être en adéquation avec ces contraintes, les dimensions supplémentaires doivent respecter deux paramètres principaux. Tout d’abord, elles doivent s’être initialement extrêmement contractées, les rendant imperceptibles à nos observations. Ensuite, elles doivent s’être stabilisées. Ce dernier paramètre signifie que l’évolution des dimensions supplémentaires doit avoir cessé très tôt dans l’évolution de l’univers, à une époque proche de la nucléosynthèse primordiale.
Une évolution dynamique des dimensions supplémentaires ferait fortement varier les constantes fondamentales de l’univers. Les auteurs montrent en effet que la valeur de ces constantes est inversement proportionnelle au taux d’expansion des dimensions supplémentaires. Plus ces dernières gagnent en taille, plus les constantes fondamentales diminuent. Or, aucun changement de ce type n’a été détecté jusqu’à maintenant. Cela implique donc nécessairement une stabilisation des DSU.
De précédents travaux ont déjà proposé un mécanisme incomplet de stabilisation dimensionnelle (12). Dans cette nouvelle étude, les auteurs proposent un mécanisme complet et cohérent avec les attentes du modèle cosmologique standard. Toutefois, tenant compte de l’extrême complexité mathématique posée par des dimensions supplémentaires complètement statiques, le mécanisme proposé ici s’applique à des dimensions évoluant très lentement (de manière quasi-négligeable).
Pour ce faire, les physiciens ont utilisé une solution particulière des équations d’état décrivant la dynamique de l’univers, cohérente avec les conditions initiales définies par le modèle cosmologique standard. Cette solution de type Kasner (la métrique de Kasner est un outil mathématique décrivant un espace-temps homogène à 4 dimensions) est une solution exacte aux équations de Friedmann (équations décrivant la dynamique de l’univers).
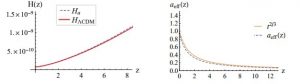
Cette solution offre un mécanisme de stabilisation dimensionnelle viable dans les premiers instants de l’univers et converge fidèlement vers l’ensemble des prédictions de la cosmologie standard. Au final, le modèle théorique ainsi proposé montre la cohérence des DSU avec l’évolution de l’univers telle que décrite par le modèle ΛCDM. Toutefois, un travail encore important reste à faire pour approfondir ce modèle et le solidifier.