Il n’est pas toujours nécessaire d’être mathématicien pour s’attaquer à certains problèmes mathématiques qui occupent les scientifiques depuis plusieurs dizaines d’années. Le biologiste Aubrey de Grey en est un parfait exemple puisque, selon un papier déposé sur le serveur de pré-publication arXiv, il aurait effectué une véritable avancée dans la résolution du problème de Hadwiger-Nelson.
En 1950, alors étudiant à l’université de Chicago, le mathématicien Edward Nelson énonce un problème d’apparence simple. Imaginez, dit-il, un graphe (un ensemble de points connectés par des lignes), assurez-vous que ces lignes soient toutes de la même longueur et que l’ensemble repose sur un plan. Maintenant, colorez chaque point, en faisant attention à ce que deux points connectés n’aient pas la même couleur. Nelson demande alors : quel est le nombre minimum de couleurs nécessaires pour colorier le plan de telle sorte que deux points séparés d’une unité soient toujours de couleurs distinctes ?
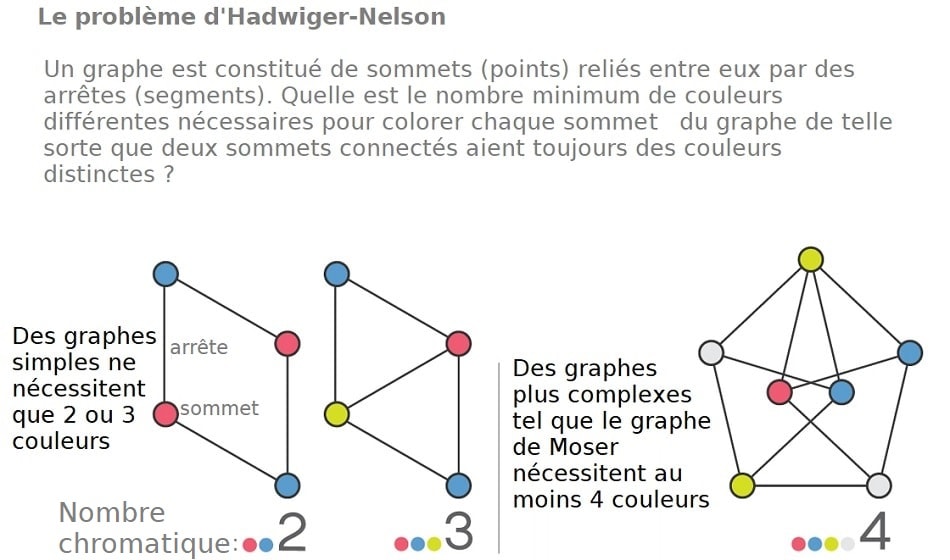
En parallèle, le mathématicien suisse Hugo Hadwiger formule une variante du problème dont il publiera l’énoncé exact quelques années plus tard. Le problème devient ainsi le problème de Hadwiger-Nelson. Celui-ci va susciter l’intérêt de mathématiciens, tel que Paul Erdős, qui vont rapidement contraindre le nombre chromatique comme étant compris entre 4 et 7 ; en d’autres termes, le graphe doit au moins être coloré avec 4 couleurs et avec 7 couleurs maximum. Bien que de nombreuses autres tentatives de contraindre plus précisément cette borne aient eu lieu, aucune n’a véritablement réussi à faire avancer la résolution du problème.
C’est là qu’intervient le biologiste et ex-informaticien britannique Aubrey de Grey. Connu pour ses propos controversés sur l’anti-vieillissement cellulaire par modification des mécanismes mitochondriaux, le scientifique a déposé la semaine dernière un papier sur le serveur arXiv intitulé « The Chromatic Number of the Plane is at least 5 » (le nombre chromatique du plan est au moins 5) et dans lequel il décrit la construction d’un graphe planaire qui ne peut être coloré avec seulement 4 couleurs. Cette contrainte plus précise de la borne initiale représente une véritable avancée dans la résolution du problème de Hadwiger-Nelson qui stagnait depuis plusieurs années.

« J’ai été extraordinairement chanceux » explique de Grey. « Ce n’est pas tous les jours que quelqu’un propose une solution à un problème vieux de 60 ans ». En effet, de Grey est parvenu à cette solution en jouant au jeu de plateau Othello. Il y a plusieurs dizaines d’années, de Grey était un jour compétitif d’Othello, il s’est intéressé au jeu de stratégie comme beaucoup de mathématiciens à l’époque. Avec eux, de Grey a appris les bases de la théorie des graphes et n’a cessé de travailler dessus depuis. « De temps en temps, lorsque j’ai besoin d’une pause dans mon véritable travail, je fais des maths ».
Bien qu’inhabituel, il n’est pas totalement rare qu’un mathématicien amateur fasse significativement avancer un problème mathématique de longue durée. Dans les années 1970, Marjorie Rice, une amateur occasionnelle de mathématiques, publie dans le journal Scientific American une solution ajoutant cinq pentagones de plus au problème du pavage du plan. Pour Gil Kalai, mathématicien à l’université hébraïque de Jérusalem, c’est une très bonne chose de voir des mathématiciens non professionnels être à l’origine d’importantes avancées. « Cela rajoute de la substance aux multiples facettes de l’expérience mathématique » confie-t-il.
Ce genre de problème n’est pas nouveau. L’un des plus célèbres est le théorème des quatre couleurs affirmant qu’il est possible, avec seulement 4 couleurs différentes, de colorier n’importe quelle carte découpée en pays (ou régions) connexes de sorte que deux pays limitrophes (partageant une frontière) aient toujours des couleurs distinctes. L’énoncé peut tout à fait s’adapter à la théorie des graphes en remplaçant les pays par des sommets et les frontières par des arrêtes reliant les sommets.
Mais le problème de Hadwiger-Nelson est un peu différent. Au lieu de considérer un nombre fini de points, comme c’est le cas avec une carte, le problème considère un nombre infini de points, c’est-à-dire chaque point du plan. Deux points sont connectés par un segment s’ils sont distants d’une unité. Pour déterminer une limite inférieure du nombre chromatique, il suffit alors de construire un graphe avec un nombre fini de sommets requérant un nombre particulier de couleurs pour respecter la condition initiale. C’est de cette façon que de Grey est parvenu à sa solution.
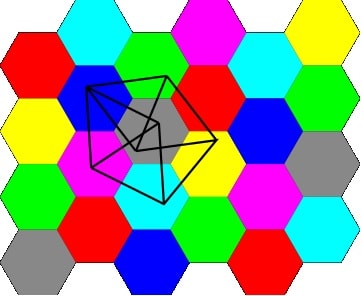
En 1961, les mathématiciens canadiens Leo et William Moser publient un article dans lequel ils présentent un graphe composé de 7 sommets et 11 arrêtes avec un nombre chromatique égal à 4 : le graphe de Moser. En se basant sur celui-ci, de Grey a assemblé plusieurs graphes de Moser, combinés à un assemblage de points supplémentaires, afin d’obtenir un graphe avec 20’425 sommets ne pouvant être colorés avec seulement 4 couleurs. Il a ensuite diminué le nombre de sommets à 1581.
La découverte d’un graphe nécessitant au minimum 5 couleurs a donc représenté une véritable avancée. Cependant, les mathématiciens ont souhaité savoir si un graphe plus petit pouvait également correspondre à cette solution. En d’autres termes, il s’agissait de trouver le plus petit graphe possible avec un nombre chromatique minimum égal à 5, dans le but d’admettre la solution de de Grey comme solution exacte du problème d’Hadwiger-Nelson. Le biologiste a donc transmis ce challenge au mathématicien Terence Tao de l’université de Californie afin qu’il soit intégré au projet Polymath.
Le projet Polymath a été lancé en 2009 par le mathématicien Timothy Gowers de l’université de Cambridge comme plateforme collaborative ouverte aux chercheurs et au public pour résoudre certains problèmes mathématiques, améliorer des résultats, vérifier des preuves, etc. Ainsi, de Grey a récemment fait partie d’une collaboration de mathématiciens ayant, grâce à Polymath, réalisé des progrès majeurs dans la résolution de la conjecture sur les nombres premiers jumeaux.

Tous les problèmes mathématiques ne correspondent pas aux conditions de Polymath, mais celui de de Grey semble être un bon candidat. En effet, le problème est facile à comprendre et les objectifs sont claires : diminuer le nombre de sommets pour un nombre chromatique minimum de 5. Depuis lundi, l’informaticien et mathématicien Marijn Heule (université du Texas) a déjà réussi à construire un graphe à 5 couleurs avec seulement 826 sommets.
Ces travaux ont relancé l’intérêt des chercheurs pour le problème de Hadwiger-Nelson. « Pour un problème tel que celui-ci, la solution finale pourrait avoir de profondes implications mathématiques » explique Gordon Royle, mathématicien à l’université d’Australie de l’Ouest. « Ou alors, cela pourrait simplement se résumer à quelqu’un d’ingénieux trouvant un graphe à plusieurs couleurs ».


