En convertissant les compositions de Johann Sebastian Bach en réseaux mathématiques, des chercheurs avancent que ces dernières contiennent de grandes quantités d’informations (au sens mathématique) et les transmettent très efficacement aux auditeurs. En outre, les œuvres du genre choral, entre autres, seraient selon eux moins informatives que celles destinées à surprendre et à divertir, telles que les toccatas. Cette nouvelle méthode d’étude mathématique de la musique pourrait aider les compositeurs dans leurs processus de création ou être appliquée à d’autres formes d’art pour quantifier le contenu informationnel.
Depuis des milliers d’années, la musique est utilisée par toutes les civilisations humaines à la fois pour divertir et pour transmettre des émotions. Il a été suggéré que bien qu’abstraite, la musique (sans paroles) est tout de même communicative et informationnelle, car notre cerveau l’analyserait en formant des attentes et de la surprise. En d’autres termes, nous aurions tendance à anticiper chaque note et ressentons de la surprise lorsqu’elle ne correspond pas à nos attentes.
En effet, d’un point de vue évolutif, notre cerveau est capable de former des attentes basées sur l’expérience ou les événements antérieurs. Lorsqu’une expérience présente est en contradiction avec ces attentes, cela provoque de la surprise, qui engendre à son tour d’autres émotions. Par exemple, nous ressentirions un soulagement lorsqu’une musique dissonante se réarrange pour redevenir plus harmonieuse, tandis qu’un sentiment de détresse surviendrait lorsque le réarrangement attendu ne se produit pas.
Cependant, la quantification de l’information véhiculée par la musique constitue un véritable défi, en raison de son côté imprévisible. Afin de surmonter ce défi, un groupe de chercheurs de l’Université de Pennsylvanie, de Yale, de Princeton et de l’Institut de Santa Fe (aux États-Unis) a développé une nouvelle technique basée sur la science des réseaux permettant de quantifier mathématiquement ces informations. L’objectif était entre autres de comprendre le lien entre la capacité d’anticiper un morceau et sa structure.
Les styles plus vifs véhiculent plus d’informations
Dans le cadre de leur nouvelle étude, récemment publiée dans la revue Physical Review Research, les chercheurs ont choisi le répertoire de Bach comme premier modèle d’analyse. Le compositeur a notamment produit un très grand nombre d’œuvres aux structures très diversifiées. De plus, ces dernières sont hautement mathématiques, et donc idéales pour ce type d’analyse, selon les scientifiques. Pour ce faire, des centaines de préludes, de fugues, de chorals, de toccatas, de concertos, de suites et de cantates, ont été sélectionnées.
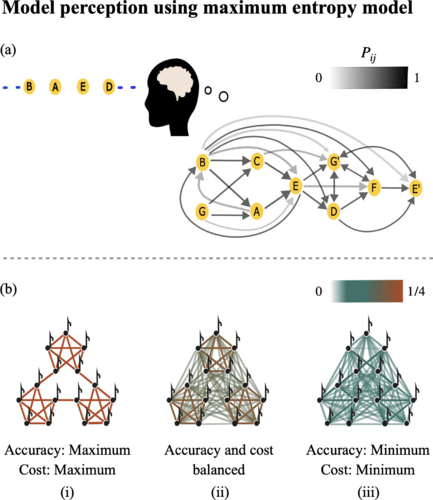
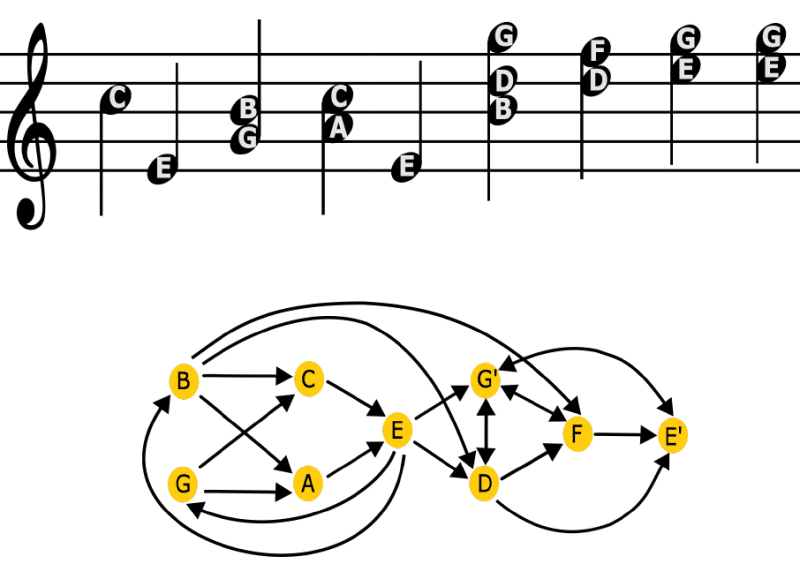
Pour traduire les morceaux en réseaux d’informations, un nœud a été attribué à chaque note et chaque transition vers la note suivante a été convertie en lignes ou arêtes reliant les nœuds entre eux. Pour quantifier les informations contenues dans les réseaux, les chercheurs ont calculé « leur entropie de Shannon ». L’entropie de Shannon correspond à la quantité d’informations contenues ou fournies par une source donnée (signal électrique, code informatique, …). Plus les informations émises sont diversifiées, plus l’entropie est grande.
À noter que des chercheurs ont précédemment déjà utilisé la théorie des réseaux pour analyser l’interconnectivité entre les notes de musique. Cependant, un aspect important de la communication, la nature imparfaite et hétérogène de la perception humaine, n’a jusqu’à présent pas été pris en compte. « Les humains apprennent de manière imparfaite », a expliqué au New Scientist l’auteur principal de l’étude, Suman Kulkarni, de l’Université de Pennsylvanie.
Le modèle développé par l’équipe intègre cet aspect, en analysant les décalages entre les réseaux déduits de la perception des auditeurs et ceux déduits informatiquement des morceaux originaux. Pour ce faire, une autre partie de l’expérience consistait à mesurer à quel point (et à quels moments) les auditeurs ressentaient de la surprise ou non, par rapport aux morceaux qu’ils écoutaient. Dans ce contexte, les liens entre chaque nœud représentaient la probabilité selon laquelle l’auditeur estime que deux notes connectées vont être jouées successivement.
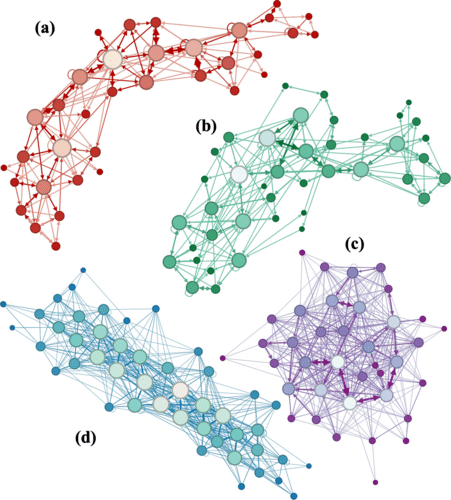
Il a été constaté que les décalages entre les deux catégories de réseaux étaient relativement faibles, ce qui signifierait que les compositions de Bach transmettent l’information de manière particulièrement efficace. Il a également été constaté que les chorals ont une entropie faible, tandis que les toccatas et les préludes ont une entropie élevée. Cela signifierait que les morceaux au rythme plus vif contiennent des informations plus diversifiées et en plus grande quantité.
Selon les experts, ces différences reflètent les fonctions de chaque style. Les chorals — des morceaux destinés aux chants en chœur — semblent simples et prévisibles, n’impliquant ainsi que peu de contenu informationnel. En revanche, les toccatas et les préludes — destinés à divertir et à surprendre — véhiculent une plus grande richesse d’informations. Par ailleurs, en analysant plus avant les variations d’entropie, il a été constaté que les compositions appartenant aux mêmes styles sont clairement regroupées dans des catégories d’entropie similaire.
Toutefois, l’équipe a précisé que le modèle d’analyse devrait encore être élargi afin de refléter une description réaliste de la musique, notamment en incluant d’autres variables telles que le rythme et le timbre (caractéristique du son qui permet de reconnaître un instrument ou une voix). Les variations de perception individuelles, par exemple entre les personnes ayant eu une formation musicale ou non, devraient également être examinées. D’autre part, il serait intéressant d’affiner le modèle en intégrant les réponses cérébrales des auditeurs et en analysant d’autres styles musicaux, de différentes cultures.
Néanmoins, cette approche pourrait déjà aider les compositeurs dans leurs processus de création, estiment les chercheurs. Par exemple, un logiciel de composition pourrait fournir des mesures d’entropie et orienter le compositeur vers des modifications pour l’amplifier ou l’atténuer. En outre, la technique pourrait être appliquée à d’autres formes d’art, telles que la littérature, afin d’analyser la capacité à transmettre des informations – ou même à des expériences interactives comme les casinos en ligne, qui utilisent des mécaniques de personnalisation et de stimulation sensorielle similaires.

