Pi est sans doute l’une des constantes les plus emblématiques des mathématiques. Il se manifeste dans les cercles, les pendules, la constante cosmologique et même dans les fameuses équations de la relativité générale d’Albert Einstein. Il figure également dans l’une des formules les plus importantes de la mécanique quantique : le principe d’incertitude d’Heisenberg. Récemment, dans le cadre de leurs travaux sur la théorie des cordes visant à mieux comprendre l’interaction des particules à haute énergie, deux physiciens ont fait une découverte stupéfiante : ils ont mis au jour une nouvelle représentation en série du nombre irrationnel pi.
Pi (π) est un nombre irrationnel contenant une infinité de chiffres, et l’un des plus grands défis associés à cette constante est d’en découvrir toujours plus. Le nombre de chiffres connus à ce jour est de 105 trillions, un record obtenu par un groupe de chercheurs de Solidigm, par le biais de l’algorithme de Chudnovsky. Une autre méthode pour déterminer les chiffres de pi est la formule de Machin, basée sur des combinaisons d’arc tangentes. De leur côté, deux scientifiques de l’Indian Institute of Science, Arnab Priya Saha et Aninda Sinha, ont découvert une toute nouvelle formule pour calculer Pi.
Saha et Sinha ne prévoyaient pas de se lancer dans une recherche d’une nouvelle équation de pi. Leur travail se concentrait principalement sur une théorie visant à unifier l’électromagnétisme, la gravité et les forces nucléaires. En effet, la théorie des cordes suggère que les éléments fondamentaux de l’univers ne sont pas des particules, mais de minuscules cordes vibrantes. Les vibrations générées par ces cordes seraient à l’origine de toute matière et de tout phénomène visible. Dans le cadre de leur étude, Saha et Sinha ont analysé comment ces cordes pouvaient interagir.
En développant une formule pour optimiser leurs calculs, ils ont découvert que celle-ci pouvait également servir à calculer pi. « Au départ, nos efforts n’étaient pas dirigés vers la recherche d’un moyen de calculer pi. Nous étudiions la physique des hautes énergies dans le cadre de la théorie quantique et cherchions à développer un modèle avec moins de paramètres et plus précis pour comprendre comment les particules interagissent. Nous avons été enthousiasmés lorsque nous avons découvert une nouvelle façon d’observer pi », explique Sinha dans un communiqué.
Une nouvelle formule similaire à celle de Madhava
La toute première série de pi enregistrée dans l’histoire (π/4 = 1 – 1/3 + 1/5 – 1/7 + …) a été établie au XVe siècle par le mathématicien indien Sangamagrama Madhava. La nouvelle formule de Saha et Sinha se rapproche de celle de Madhava, mais dans une certaine mesure uniquement. Pour y parvenir, les physiciens ont combiné la fonction Euler-Beta avec le diagramme de Feynman. Ils affirment que cette nouvelle formule permet une détermination de pi plus précise.
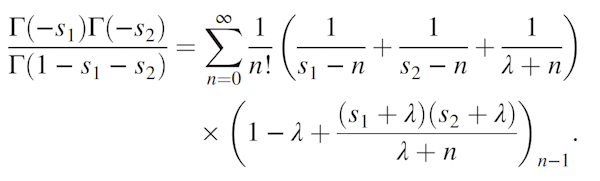
Le duo a également expliqué, dans leur étude publiée dans la revue Physical Review Letters, que leur formule, produisant un chiffre infiniment long, dépend du facteur λ (un paramètre librement choisi). Selon les physiciens, quelle que soit la valeur de λ, la formule aboutit toujours à π. Ils ont également souligné que la formule de Madhava est très « lente » à converger, nécessitant 100 termes pour atteindre 0,01 de pi. En revanche, leur représentation permet de calculer pi à 10 chiffres avec seulement 30 termes. « Alors que la série de Madhava nécessite 5 milliards de termes pour converger à 10 décimales, la nouvelle représentation avec λ entre 10 et 100 en nécessite seulement 30 », ont-ils déclaré.
L’étude des séries mathématiques revêt une grande importance en physique, car ces dernières sont essentielles pour diverses simulations informatiques. Avec cette nouvelle formule, Saha et Sinha ont accéléré le processus. Le duo a également accompli un exploit en développant une nouvelle méthode indiquant la probabilité que deux cordes fermées interagissent.

