Depuis plusieurs années, les physiciens savent que dans certaines situations, la matière peut être placée dans un état très proche de l’immobilité. C’est par exemple le cas du condensat de Bose-Einstein, un état particulier de la matière à très basse température où la quantité de mouvement des atomes est drastiquement réduite. Mais l’immobilité totale est-elle possible ?
Dans un précédent article, nous relations les résultats d’une étude publiée par l’University College London démontrant l’impossibilité d’atteindre le zéro absolu et, par conséquent, l’immobilité complète, en vertu du troisième principe de la thermodynamique. Cependant, quelques dizaines d’années auparavant, le physicien Werner Heisenberg démontrait déjà l’impossibilité pour la matière d’être totalement immobile, au moyen de son célèbre principe d’indétermination.
Les relations d’indétermination d’Heisenberg
En 1927, le physicien Werner Heisenberg introduit son principe d’indétermination énonçant l’impossibilité de mesurer simultanément, avec une précision identique, deux propriétés physiques d’un système quantique (une particule par exemple). Plus exactement, lorsque la précision sur la mesure d’une propriété s’accroît, la précision sur la mesure de l’autre propriété diminue corrélativement.
Initialement, Heisenberg démontre cette impossibilité pour deux propriétés physiques (appelées des « variables complémentaires » en mécanique quantique) en particulier : la position « x » et la quantité de mouvement « p ». La quantité de mouvement étant le produit de la masse par la vitesse, noté p = mv. Il est ainsi fréquent de voir le principe d’Heisenberg résumé par la phrase suivante : « il est impossible de connaître précisément la position et la vitesse d’une particule ».
Le physicien américain Earle Hesse Kennard a formalisé ce principe en utilisant la notion statistique d’écart-type, noté « σ ». Pour rappel, en statistique, la dispersion d’une variable désigne la variabilité des valeurs que peut prendre une variable. Ainsi, une dispersion nulle signifie qu’il existe une valeur précise pour cette variable. Au contraire, une très grande dispersion signifie qu’il est impossible de fixer une valeur précise.
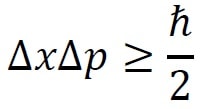
Appliqué au principe d’indétermination, cela signifie que si la quantité de mouvement est précisément mesurée, c’est-à-dire que sa dispersion est nulle, alors la position est très imprécise (sa dispersion serait nécessairement maximale).
Principe d’indétermination et immobilité
La position et la quantité de mouvement d’une particule évoluent en fonction de sa dynamique. Lorsque l’on ralentit progressivement une particule, la vitesse de celle-ci, et donc la quantité de mouvement, diminue. De la même manière, plus une particule ralentit et plus sa position se stabilise. Ainsi, quand une particule est très fortement ralentie, il devient possible de connaître avec une précision croissante sa position et sa vitesse (qui tend vers zéro).
Dans le cas d’une particule totalement immobile, la dispersion sur la position est nulle (la position est exactement connue). De même, la dispersion sur la quantité de mouvement est également nulle (la vitesse est exactement connue, elle est égale à zéro). Pour une particule immobile, les variables complémentaires « position » et « quantité de mouvement » ont une dispersion nulle et sont donc simultanément connues avec la même précision.
Or, la relation d’indétermination d’Heisenberg énonce que si la dispersion sur une variable est nulle, la dispersion sur l’autre variable doit obligatoirement être maximale. En d’autres termes, il est fondamentalement impossible de mesurer simultanément avec une égale précision deux variables complémentaires d’une même particule.

Il est donc impossible pour une particule d’être immobile sans violer la limite fondamentale posée par Heisenberg. Dès lors, une particule ne peut jamais se trouver dans un état totalement immobile, elle conserve en permanence une quantité de mouvement, même infinitésimale, de manière à ce que la dispersion sur celle-ci ne soit jamais strictement nulle, et donc jamais parfaitement connue.

