Deux trous noirs intriqués quantiquement pourraient être reliés par un trou de ver à la structure segmentée et bosselée, dite « chenille d’Einstein-Rosen », suggère un nouveau modèle mathématique. Alors que les précédentes théories, popularisées par le cinéma de science-fiction, évoquaient un tunnel lisse et régulier, ce modèle décrirait plutôt une structure spatio-temporelle reflétant les caractéristiques aléatoires et chaotiques propres aux trous noirs.
L’intérieur des trous noirs reste l’un des grands mystères de la physique moderne, la gravité y étant si extrême que même la lumière ne peut s’en échapper. Cela signifie que les processus internes échappent à toute observation directe : nos instruments astronomiques ne peuvent capter que la lumière émise par les disques d’accrétion, zones périphériques où la matière rayonne encore.
De nombreuses théories ont tenté d’en percer le secret. Certaines avancent qu’une unification de la relativité générale d’Einstein et de la mécanique quantique – un défi que les physiciens s’efforcent de résoudre depuis des décennies – permettrait de modéliser l’intérieur des trous noirs. Autrement dit, cela exigerait une théorie complète de la gravité quantique, qui n’a pas encore été formulée.
Les modèles mathématiques proposés jusqu’ici montrent que la taille intérieure d’un trou noir serait proportionnelle à sa complexité, c’est-à-dire à celle de ses constituants quantiques. Les chercheurs se sont donc demandé si cette règle pouvait également s’appliquer aux trous de ver reliant deux trous noirs. En effet, un trou de ver reliant deux trous noirs quantiquement intriqués pourrait offrir un aperçu de leur intérieur.
Les trous de ver, ou ponts d’Einstein-Rosen, sont des tunnels reliant deux points éloignés de l’espace-temps. Dans l’intrication quantique, deux particules formant une « paire d’Einstein-Podolsky-Rosen » demeurent inextricablement liées, quelle que soit la distance qui les sépare. Certains physiciens ont suggéré que ces deux phénomènes pourraient être équivalents dans le cas de deux trous noirs intriqués.
Le nouveau modèle mathématique, élaboré par des chercheurs de l’Université Brandeis (Massachusetts) et de l’Institut Balseiro (Argentine), confirme en partie cette hypothèse. En modélisant deux trous noirs intriqués, ils ont observé que les processus mis en jeu seraient bien plus complexes qu’on ne le pensait.
Un trou de ver stable reliant deux trous noirs chaotiques
Pour décrire mathématiquement l’intérieur d’un trou de ver reliant deux trous noirs intriqués, les chercheurs ont mis au point un modèle reliant partiellement la physique quantique et la gravité. Bien que cette approche reste incomplète, elle s’avère suffisamment réaliste pour reproduire certains processus physiques. « À quoi ressemblent les états intriqués typiques de deux trous noirs ? Contiennent-ils des intérieurs semi-classiques ? Nous abordons ces questions de manière constructive, en proposant des ensembles d’états explorant de manière dense l’espace de Hilbert [un espace vectoriel réel doté d’un produit scalaire euclidien] du trou noir », expliquent-ils dans leur article récemment publié dans Physical Review Letters.
Les chercheurs ont d’abord développé un modèle théorique simplifié d’un trou de ver lisse et régulier, reposant sur un état quantique ordonné reliant les deux trous noirs. Ils ont ensuite simulé, par calcul, une paire de trous noirs chaotiques dont l’état d’intrication était volontairement brouillé, avant d’en déduire la géométrie du trou de ver correspondant.
Les simulations indiquent que, pour conserver la stabilité du système malgré le désordre quantique, le trou de ver devrait être long, sinueux et présenter des irrégularités de matière, rappelant le corps d’une chenille – d’où l’appellation « chenille d’Einstein-Rosen ». Ces résultats mettent en évidence un lien mathématique direct entre le chaos quantique des trous noirs et la structure du trou de ver.
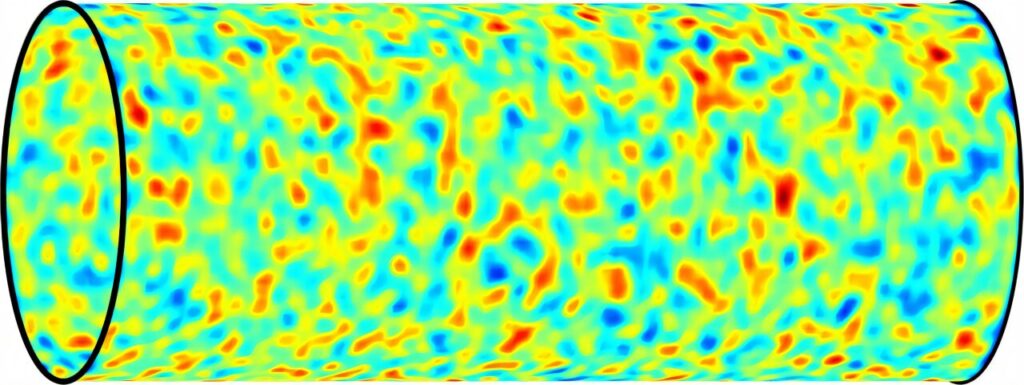
La chenille d’Einstein-Rosen est un long trou de ver bosselé, soutenu par une distribution de matière inhomogène. © Javier M. Magán et al.En d’autres termes, plus l’état quantique des trous noirs est aléatoire et chaotique, plus le trou de ver qui les relie devient complexe. « L’ensemble des chenilles ER de longueur moyenne ℓ et d’échelle de corrélation de matière ℓΔ forme un état quantique k ε-approximatif des trous noirs pour k ~ (ℓ − ℓε) / ℓΔ », précisent les chercheurs.
Ces résultats pourraient avoir des implications majeures pour certaines théories comme le « paradoxe du pare-feu ». Ce dernier postule que l’intérieur d’un trou noir ne serait ni lisse ni stable, l’espace-temps pouvant se rompre à sa périphérie sous l’effet d’un rideau d’énergie appelé « pare-feu ». Le nouveau modèle suggère au contraire que, même lorsque l’intrication quantique est chaotique et aléatoire, le trou de ver pourrait rester stable, les lois classiques de la gravité continuant à s’y appliquer.
