Comme nous le savons depuis qu’Einstein nous l’a décrit par le biais de la théorie de la relativité générale, l’espace, ou plus précisément l’espace-temps, se courbe en présence d’un corps de masse importante. En d’autres termes, celui-ci se courberait en présence d’une planète, d’une étoile ou tout autre corps, et ce proportionnellement à sa masse.
Cette théorie fut une véritable révolution puisqu’elle vint remplacer pour ce genre d’applications la théorie de la gravité universelle de Newton, qui postule que la gravitation n’est autre qu’une force générée par un corps possédant une masse X. Or, la théorie de la relativité vient nous dire qu’il ne s’agit pas d’une force, mais d’une déformation du tissu de l’espace-temps.
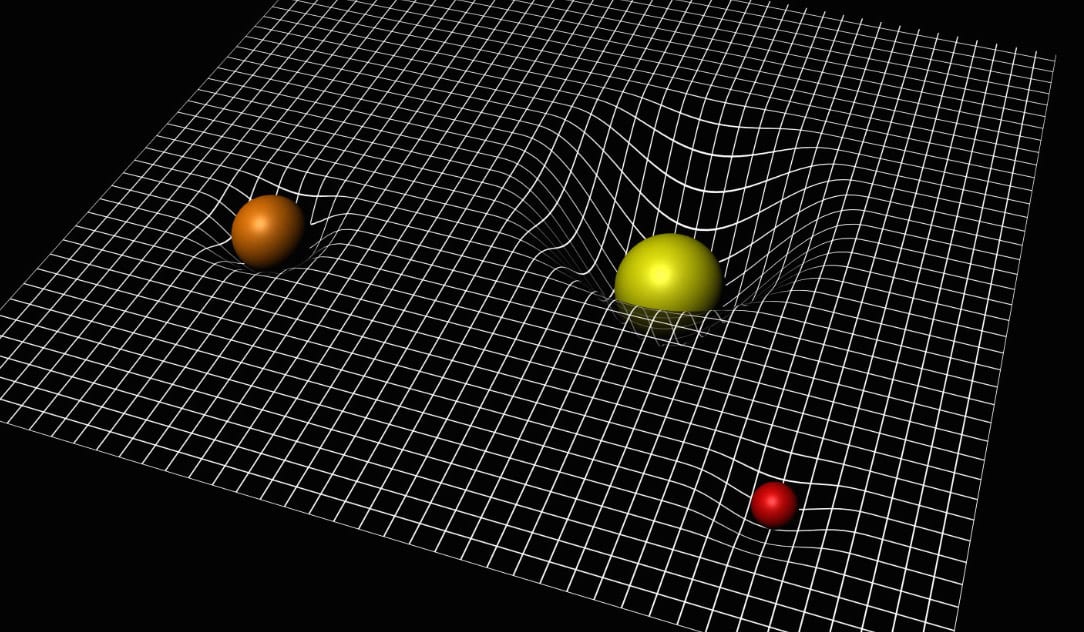
Pour le comprendre, il vous suffit soit de regarder l’image ci-dessous, soit de vous imaginer la chose suivante : admettons que vous possédiez une nappe au tissu légèrement élastique. Tout en maintenant la nappe tendue bout à bout, vous viendriez déposer une boule de billard en son centre. Le tissu s’adapterait alors au poids de la boule subissant l’effet de la gravité en adoptant une forme qui épouse sa géométrie.
Cette déformation est donc proportionnelle à la masse de notre boule de billard. Si vous imaginez maintenant une autre boule, cette fois entièrement composée de plomb (et donc bien plus lourde), la déformation résultante sera d’autant plus importante. Autrement dit, la déformation du tissu est proportionnelle à la masse du corps la provoquant.
Bon, tout cela s’appliquait à un bout de tissu et une vulgaire nappe… Concernant le « tissu de l’espace-temps » et l’influence conséquente à la présence d’un corps céleste, les mécanismes en jeu sont en réalité bien plus complexes. Premièrement, la déformation d’un tel espace ne se produit pas de manière tridimensionnelle comme cela est le cas pour notre expérience. Ici, nous parlons de conséquences en 4 dimensions, soit : les axes d’un référentiel espace-temps [x,y,z,t], « t » étant l’axe représentant la dimension du temps.
Une façon de schématiser un espace relativiste est la représentation de Minkowski (espace de Minkowski). Deuxièmement, la « déformation » n’est pas directement due à la masse tirée vers le bas en raison de la gravité, puisque c’est cet objet même qui génère la force gravitationnelle. Autrement dit, selon Einstein, la déformation de l’espace-temps dépend de l’énergie contenue dans le corps concerné, plus précisément, à son énergie divisée par le carré de la vitesse de la lumière. Serions-nous en train de décrire E/c2 ? Tiens donc, cela ressemble étrangement à E=mc2 !
Mais, est-ce que cette déformation de l’espace-temps est due à l’influence d’une masse céleste, avec tous les phénomènes physiques qu’elle génère ? Ou alors, est-elle due à l’énergie concentrée en ce seul et même endroit ? Autrement dit, bien que nous connaissions l’équivalence relativiste mathématique entre énergie et matière, d’un point de vue fondamental, ce sont deux choses bien différentes.
Pour vous imager un tel questionnement : si nous parvenions à extraire toute l’énergie d’un trou noir par exemple, en l’isolant de sa masse (bien que cela paraisse absurde) afin de la placer quelque part d’autre au sein de l’espace, l’espace-temps en serait-il toujours courbé ? La théorie de la relativité nous dit d’office que cela est absurde puisque selon la formule, qui s’applique uniquement à des particules au repos, toute énergie de masse nulle ne peut par conséquent pas être au repos. Le photon par exemple, dit de masse nulle, possède une énergie, mais également une vitesse constante, celle de la lumière « c », soit environ 300’000 km/s.
Très bien, vu comme cela, admettons que l’énergie sans masse que nous venons de déposer dans l’espace soit en mouvement, mais dans un mouvement circulaire et sans dispersion d’énergie. Que se passerait-il alors ? L’espace-temps en serait-il déformé, ne serait-ce que l’espace d’un instant avant la dispersion de cette énergie ? Cette expérience de pensée peut paraître absurde étant donné qu’elle n’entre plus dans le cadre de la relativité générale et que c’est elle qui prédit justement la déformation de l’espace-temps par la présence d’un corps possédant une certaine masse. Mais il s’agit d’une réflexion intéressante qui chatouille peut-être les limites de cette théorie…
Une telle expérience, en appliquant une logique relativiste et mathématique, ne donnerait donc pas lieu à la déformation de l’espace-temps. De plus, une telle expérience nous est impossible à concevoir, car nous ne saurions comment y parvenir. Mais, si la nature nous confiait ses pouvoirs, juste le temps de tenter l’expérience, que se passerait-il ? À méditer…
Voici maintenant une petite question pour vous :
Étant donné que selon Einstein, une masse, au repos, peut être exprimée par E/c2 et que nous savons que la déformation de l’espace-temps dépend de la masse, laquelle/lesquelles de ces affirmations est/sont correcte(s) ?
- La déformation de l’espace-temps dépend de la masse.
- La déformation de l’espace-temps dépend de l’énergie.
- Les deux affirmations ci-dessus sont justes puisqu’en raisonnement relativiste, masse = énergie / (vitesse de la lumière)2.
- Les poneys roses sont gentils et je ne comprends plus rien moi avec tout ça.
- Aucune des réponses ci-dessus n’est correcte.


