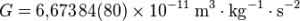Les trous noirs s’évaporent naturellement : le rayonnement de Hawking

Saviez-vous que les trous noirs s’évaporent et qu’ils ne sont en fait pas totalement noirs ? Selon la théorie développée par le grand physicien Stephen Hawking, ils seraient légèrement luisants et constamment en train d’émettre des particules par intensité faible depuis leur surface. Il s’agit du rayonnement de Hawking, prédit par le physicien en 1975 dans le cadre de l’un de ses plus importants travaux.

Ce rayonnement est en réalité d’une intensité extrêmement faible et varie selon le type de trou noir. Elle est le plus faible pour les trous noirs dits supermassifs ou intermédiaires et plus importante pour ceux issus de l’évolution stellaire. À l’heure actuelle, il faut savoir qu’il est impossible de prouver directement ce rayonnement (par l’observation).

Une telle observation pourrait cependant potentiellement être réalisée dans le cadre d’expérimentations rendues possibles par le biais d’accélérateurs de particules. En effet, ces « trous noirs primordiaux » ainsi générés, comme tel a théoriquement été le cas lors du Big Bang, pourraient être produits dans des appareils tel que le LHC (accélérateur de particules du Cern).

Le rayonnement de Hawking

La théorie quantique des champs (mécanique quantique appliquée dans le cadre de la relativité restreinte) explique l’existence des fluctuations du vide. C’est à dire, l’existence de paires particule-antiparticule qui sont en permanence générées par le vide.

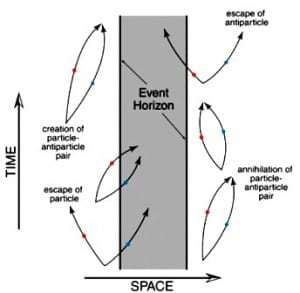
Le diagramme espace-temps ci-dessus, réalisé par la Northern Arizona University, démontre le principe du rayonnement Hawking. L’on constate tout de suite les éléments essentiels qui sont issus d’un phénomène particule-antiparticule. Les particules apparaissent avant de s’annihiler entre elles.

Le vide quantique varie sans cesse. Comme on peut le voir sur le schéma, il arrive que l’une des particules se fasse « aspirer » par le trou noir lorsqu’elle s’approche suffisamment de son horizon des événements. Le phénomène à l’origine de la séparation des paires de particules est appelé « force de marée ».

Les forces de marée générées par les champs gravitationnels agissant sur les paires de particules fournissent l’énergie nécessaire à la séparation, ce qui engendre une perte d’énergie du trou noir et qui fait finalement diminuer sa masse en raison de la perte de particules. Tout cela est bien entendu extrêmement faible mais prouve tout de même que les trous noirs se dégradent naturellement.

D’ailleurs, plus le trou noir est petit, plus ces forces de marée sont importantes. La quantité de rayonnement Hawking augmente alors et devient plus rapide. Un petit trou noir de la masse d’une montagne devrait donc s’évaporer rapidement en conséquence d’un rayonnement de particules élevé. Les principales particules dégagées sont les photons gamma, les neutrinos ainsi que les positrons.

Bonus : calcul de la masse, de la durée de vie et de la température d’un trou noir !

Pour les plus curieux, nous proposons quelques détails de calcul en s’appuyant sur les différentes formules issues du travail de Stephen Hawking. Pour l’exemple, nous avons calculé la température (en Kelvin) ainsi que la durée de vie (temps d’évaporation) d’un trou noir de Schwarzschild faisant la taille d’un ballon de foot standard (taille 5).

Nous avons choisi le trou noir de Schwarzschild, car il permet une relation simple entre sa masse et son rayon. Ce qui nous permet, à partir du simple rayon d’un ballon de football, de calculer la masse estimée du trou noir afin d’effectuer la suite des calculs.

Commençons par poser les données et les formules

Rayon du trou noir « R » : 11 cm (ballon de football)

Les formules

[column size=one_third position=first ]1) Gravité de surface :[/column]

[column size=one_third position=middle ]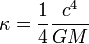[/column]

[column size=one_third position=last ][/column]

 

[column size=one_third position=first ]2) Rayon du trou noir :[/column]

[column size=one_third position=middle ]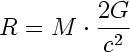[/column]

[column size=one_third position=last ][/column]

 

[column size=one_third position=first ]3) Temps d’évaporation du trou noir :[/column]

[column size=one_third position=middle ]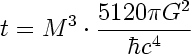[/column]

[column size=one_third position=last ][/column]

 

[column size=one_third position=first ]4) Température thermodynamique du trou noir (en Kelvin) :[/column]

[column size=one_third position=middle ]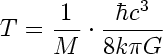[/column]

[column size=one_third position=last ][/column]

Les constantes

Constante de Planck réduite :

Constante gravitationnelle de Newton :

Vitesse de la lumière dans le vide : c = 299 792 458 m/s

Calcul

Maintenant que nous avons tout ce qu’il nous faut, voici comment procéder au calcul :

• Pour commencer, nous calculons la masse M du trou noir à l’aide de la formule « 2 » qui nous donne la relation entre le rayon R (connu) et la masse.
• Une fois la masse obtenue, on peut calculer la gravité de surface du trou noir à l’aide de « 1 ».
• Nous avons maintenant toutes les valeurs pour le calcul de la température du trou noir ainsi que de son temps d’évaporation grâce aux formules « 3 » et « 4 » !

Les résultats

1) La masse M du trou noir est de :

M = 7.41 x 10^22 tonnes, soit 12.4 fois la masse de notre Terre !

2) La température d’un tel trou noir (de petite taille) est légèrement plus élevée que celle d’un trou noir intermédiaire, la preuve, le résultat nous donne :

T = 0.001656559 Kelvin (contre 0.00000000062 Kelvin pour un trou noir faisant 100 masses solaires). Pour information, 0 Kelvin = -273.15 °C. Cela correspond au zéro absolu (température la plus basse qui puisse exister).

3) Le temps d’évaporation du trou noir finalement obtenu est d’environ (avec incertitudes) :

t = 1.083140 x 10^54 années. Cela fait beaucoup d’années !

Il est finalement intéressant de noter que même pour ce genre de trous noirs de très petite taille, la théorie nous indique, bien qu’avec quelques incertitudes, la durée de vie pratiquement infinie d’un tel objet. En réalité, si le trou noir est suffisamment massif (T < 2.726 Kelvin, ou de masse M > 0,75% de la masse de la Terre) il grandira déjà légèrement en se nourrissant du rayonnement de fond cosmique.

Pour un tel cas, ce serait uniquement si l’environnement du trou noir se refroidirait jusqu’à atteindre une température inférieure à sa température T (de Hawking) que celui-ci commencerait à s’évaporer.

Source : futura-sciences / Formules : wikipedia