Les fermions constituent, à côté des bosons, l’une des deux grandes familles de particules définies par le Modèle Standard. Ce sont des particules, élémentaires ou composites, dotées d’un spin demi-entier et obéissant à la statistique de Fermi-Dirac. Classiquement, les fermions sont considérés comme les particules de matière, tandis que les bosons sont les particules des interactions fondamentales. Le terme « fermion » a été introduit par le physicien Paul Dirac en référence au physicien italien Enrico Fermi.
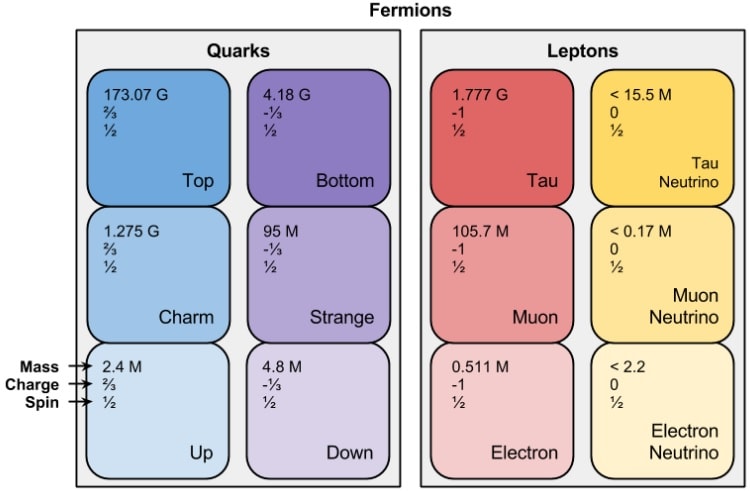
Les fermions peuvent être des particules élémentaires ou des particules composites (protons, neutrons, hypérons, etc). Les fermions élémentaires se divisent en deux catégories : les leptons — tels que l’électron et le neutrino — insensibles à l’interaction forte, et les quarks, sensibles aux quatre interactions fondamentales. Au total, le Modèle Standard compte 24 fermions répartis en trois générations : 6 leptons, 6 quarks et leurs 12 antiparticules.
Pour approfondir :
Une nouvelle mesure ultra-précise de la masse du proton
La famille des leptons contient les neutrinos (trois au total), l’électron, le muon et le tauon. Quant à la famille des quarks, elle contient le quark up (u), le quark down (d), le quark top (t), le quark bottom (b), le quark strange (s) et le quark charm (c). En plus de posséder une charge électrique, les quarks ont une charge de couleur qui les rend sensibles à l’interaction nucléaire forte. Chaque lepton et quark possède une antiparticule — des expériences étant actuellement en cours afin de déterminer si le neutrino est une particule de Majorana ou non.
De la statistique de Fermi-Dirac au principe d’exclusion de Pauli : les propriétés quantiques des fermions
La distribution statistique des fermions répartis sur différents états d’énergie d’un système en équilibre thermodynamique est donnée par la statistique de Fermi-Dirac, introduite en 1926 par les physiciens Enrico Fermi et Paul Dirac. Ainsi, lorsque deux fermions sont échangés, l’état quantique du système change de signe (fonction d’onde antisymétrique). Ce phénomène est lié au théorème spin-statistique assignant un spin demi-entier aux fermions et un spin entier aux bosons.
Ceci implique la soumission des fermions au principe d’exclusion de Pauli formulé par le physicien Wolfgang Pauli en 1925. Selon ce principe, deux fermions ne peuvent se trouver simultanément dans le même état quantique. L’état quantique d’une particule étant défini par ses nombres quantiques, il est donc interdit à deux fermions d’un même système de posséder des nombres quantiques identiques.
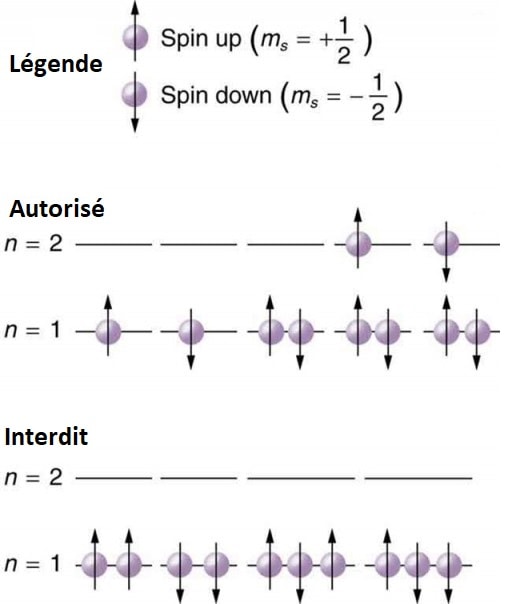
Ce principe joue un rôle crucial puisqu’il détermine la répartition des électrons sur les différentes couches électroniques d’un atome et intervient également dans la matière dégénérée ainsi que sur la pression de dégénérescence à l’intérieur des naines blanches et des étoiles à neutrons.
La théorie quantique des champs prédit trois types de fermions : les fermions de Dirac (fermions massifs), les fermions de Weyl (fermions de masse nulle) dérivés de l’équation de Dirac, et les fermions de Majorana (fermions qui sont leur propre antiparticule).
Actuellement, aucun fermion de Weyl isolé ou de Majorana n’a été expérimentalement observé ; les fermions du Modèle Standard sont tous considérés comme des fermions de Dirac obtenant leur masse — pour les fermions élémentaires — via leur couplage avec le champ de Higgs.
Dans certaines conditions, des fermions peuvent se comporter comme des bosons et obéir à la statistique de Bose-Einstein.
Supraconductivité, théorie BCS et paires de Cooper : quand les fermions deviennent des bosons
Dans le cas de la supraconductivité, les physiciens John Bardeen, Leon Neil Cooper et John Robert Schrieffer, ont introduit en 1957 la théorie BCS et notamment la notion de paires de Cooper.
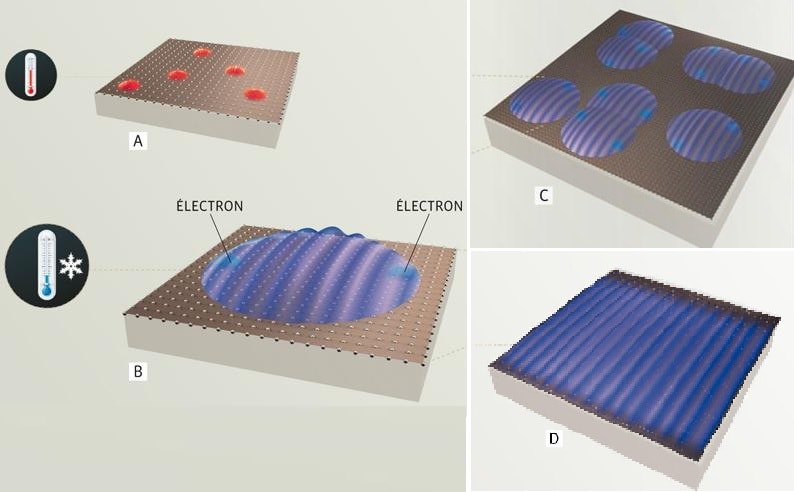
Les paires de Cooper sont des paires d’électrons liées grâce aux interactions électron-phonon ; un électron possédant un spin demi-entier (1/2), une paire d’électron possède donc un spin entier et se comporte comme un boson. Dès lors, cette configuration bosonique n’est plus soumise au principe d’exclusion de Pauli et le fait que les paires de Cooper puissent ainsi se retrouver dans le même état quantique fondamental est à la base de la supraconductivité. Le même phénomène est observé dans le cas de la superfluidité.


 L’électron est une particule élémentaire qui, avec les protons et les neutrons, constitue les atomes. C’est donc l’un des composants principaux de la matière baryonique. À ce titre, il revêt... [...]
L’électron est une particule élémentaire qui, avec les protons et les neutrons, constitue les atomes. C’est donc l’un des composants principaux de la matière baryonique. À ce titre, il revêt... [...]