Détection d’un couplage gravitationnel entre deux minuscules masses

Bien qu’elle soit l’objet d’une des plus grandes théories physiques jamais énoncées — la théorie de la relativité générale d’Albert Einstein, la gravité reste l’une des interactions fondamentales les moins bien connues. Avec une intensité mystérieusement plus faible que celle de l’interaction électromagnétique et une description d’apparence impossible en termes quantiques, la gravité comporte encore de nombreuses zones d’ombre. Récemment, des physiciens sont parvenus à détecter le champ gravitationnel généré par deux minuscules masses de 90 mg. Une prouesse qui pourrait ouvrir la voie à la détection d’effets gravitationnels quantiques.

Quatre forces fondamentales sont connues en physique : les interactions faible et forte, et les forces électromagnétique et gravitationnelle. La force gravitationnelle est la plus faible de ces quatre. Pour cette raison, et parce que les expériences ne peuvent pas être protégées de la gravité terrestre, les mesures du champ gravitationnel d’un objet sont difficiles à faire en laboratoire. Même pour des objets qui ont des masses de plusieurs kilogrammes.

Mais dans la revue Nature, Westphal et ses collègues rapportent la détection du couplage gravitationnel entre deux masses d’environ 90 milligrammes seulement.

Les interactions faible, forte et électromagnétique ont été unifiées dans le modèle standard de la physique, mais la force gravitationnelle ne peut pas être intégrée dans ce modèle. Le meilleur modèle actuellement disponible pour décrire la gravité est la théorie de la relativité générale. Cette théorie n’a échoué à aucun test jusqu’à présent, toutefois, elle se montre incompatible avec une description en termes quantiques.

Loi de la gravitation universelle de Newton : efficacité et limites

Dans la majorité des cas, cependant, nous n’avons pas besoin d’utiliser la théorie de la relativité générale pour décrire la gravité — la loi de la gravitation universelle d’Isaac Newton fonctionne parfaitement. Publiée en 1687, la loi de Newton stipule que l’attraction gravitationnelle entre deux corps est proportionnelle à leur masse et inversement proportionnelle au carré de la distance qui les sépare. Cela s’est avéré correct non seulement pour décrire la plupart des observations astronomiques, mais aussi dans les expériences de laboratoire.

Par exemple, la trajectoire d’un objet tombant librement (comme une pomme tombant d’un arbre) peut être mesurée avec une précision inférieure à dix parties sur un milliard, et les résultats sont en bon accord avec ce que l’on attendrait de la loi de Newton.

Au cours du XXe siècle, cependant, des doutes sont apparus sur l’exactitude générale de cette loi : une distribution de vitesse anormale des étoiles dans les galaxies a été observée au début des années 1930, et ne pouvait être expliquée par la seule loi de Newton. Même la théorie de la relativité générale ne peut rendre compte de ce phénomène. Une explication est de postuler l’existence de la matière noire : une composante invisible, mais génératrice de gravité, de l’Univers. Cependant, personne ne sait vraiment de quoi est faite cette matière noire.

Une autre explication, controversée mais plus facile à intégrer dans les modèles que la matière noire, est que la loi gravitationnelle de Newton a besoin d’une correction. Une théorie qui tente une telle correction a été proposée dans les années 1980 et est appelée dynamique newtonienne modifiée (MOND). La base de cette théorie est que l’intensité du champ gravitationnel (l’accélération due à la gravité) ne suit pas la loi du carré inverse de Newton sur de grandes distances.

Problème de hiérarchie et variation des mesures de G

Un autre mystère est que la force gravitationnelle est d’environ 36 ordres de grandeur plus faible que la force électromagnétique. C’est ce qu’on appelle le problème de la hiérarchie. Un cadre connu sous le nom de théorie des cordes, qui a été développé en partie pour fournir une description quantique théorique de la gravité, aborde ce problème en proposant qu’il y ait plus de dimensions spatiales que les trois que nous pouvons observer.

La gravité — contrairement aux trois autres forces fondamentales — est supposée imprégner ces dimensions supplémentaires. Si cela est vrai, cela pourrait expliquer pourquoi la force gravitationnelle est tellement plus faible que la force électromagnétique. Une autre conséquence serait que, sur une certaine plage spatiale, la force gravitationnelle ne peut pas être décrite par la loi du carré inverse de Newton.

Une autre particularité de la gravité est que les mesures indépendantes de la constante gravitationnelle de Newton (G, une constante fondamentale utilisée dans les calculs des effets gravitationnels) ont largement varié. Les déterminations expérimentales d’autres constantes fondamentales, telles que la constante de Boltzmann ou la vitesse de la lumière, ont convergé à mesure que le nombre et la précision des mesures augmentaient. Cela ne s’est pas produit pour G.

Mesurer G grâce à une balance de torsion miniature

Les expériences de Westphal et de ses collègues pourraient apporter des informations supplémentaires pour mieux comprendre la gravité. Ils ont étudié la force gravitationnelle à l’aide d’une version miniature d’une balance de torsion — un appareil qui a été utilisé pour la première fois par Henry Cavendish en 1798 pour mesurer la densité de la Terre (une expérience qui équivaut à mesurer G), et qui est toujours l’appareil de référence pour déterminer G.

Une balance de torsion se compose d’une barre horizontale suspendue au milieu à un fil suspendu verticalement, et avec des masses tests attachées aux extrémités. L’attraction gravitationnelle de la Terre agit dans la direction verticale, le long de laquelle le fil a une grande rigidité. Mais dans le sens horizontal, le fil est facilement tordu et a une petite constante de ressort — des forces très faibles appliquées à angle droit par rapport à la barre provoquent de grandes rotations de la barre.

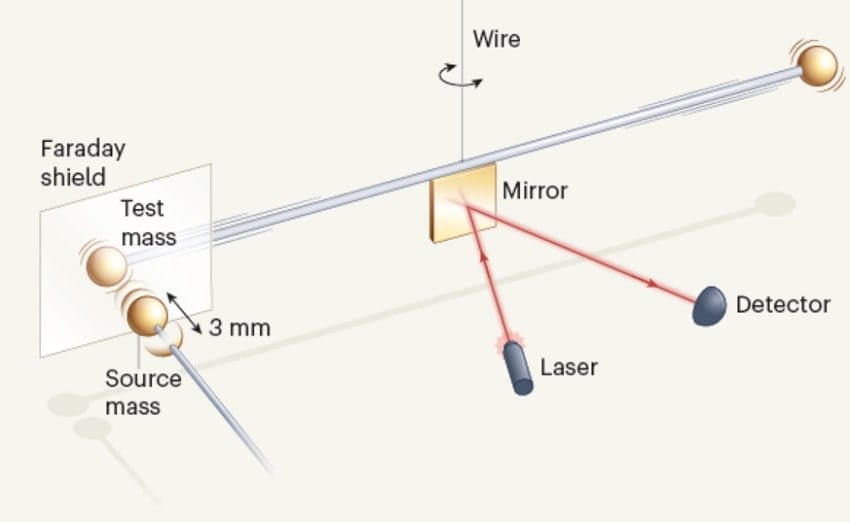
La balance génère donc un environnement presque sans gravité (plus précisément décrit comme une microgravité) dans le plan horizontal. C’est parfait pour détecter de petites forces, telles que l’attraction gravitationnelle exercée sur la barre par un objet proche (la masse source). Dans les déterminations typiques de G, les masses sources étaient lourdes (plusieurs kilogrammes), pour compenser la faiblesse de la force gravitationnelle.

Détecter le couplage gravitationnel au milieu du bruit de fond

En revanche, Westphal et ses collègues n’ont utilisé que des sphères d’or de 92 milligrammes, soit environ la masse de 4 mouches domestiques. Il s’agit de la masse source la plus faible jamais utilisée dans une telle expérience. Un calcul utilisant la loi de gravitation de Newton montre que la force agissant entre deux masses sphériques de 90 mg avec une séparation du centre de masse de 2.5 millimètres (approximativement les paramètres de l’expérience de Westphal et de ses collègues) n’est que d’environ 9×10^–14 newtons.

C’est à peu près la même force qui agit sur une masse de 9 picogrammes (1 pg équivaut à 10^–12 g) dans le champ de gravité terrestre ; pour mettre cela en perspective, 9 pg fait environ un tiers de la masse d’un globule rouge humain. Le grand défi était donc d’extraire ce signal gravitationnel extrêmement petit du bruit de fond de l’expérience et des effets d’autres forces (telles que les interactions électromagnétiques), qui deviennent plus fortes que les forces gravitationnelles lorsque la source et les masses d’essai sont séparées par de petites distances.

Les auteurs ont donc modulé le signal en faisant varier périodiquement la position de la masse source par rapport à la masse d’essai dans la balance de torsion. En conséquence de l’interaction gravitationnelle dépendant du temps, le balancier a oscillé dans le plan horizontal à la fréquence de la modulation du signal (12.7 millihertz).

Validité de la loi de la gravité de Newton pour de très faibles masses

Parce que le champ gravitationnel d’une masse sphérique est non linéaire (une conséquence de la loi du carré inverse de Newton), la balance est également stimulée pour osciller à des fréquences plus élevées qui sont des multiples de la fréquence de modulation (appelées harmoniques supérieures). Cet effet a pu être clairement identifié dans l’expérience, fournissant ainsi une signature du couplage gravitationnel entre les masses.

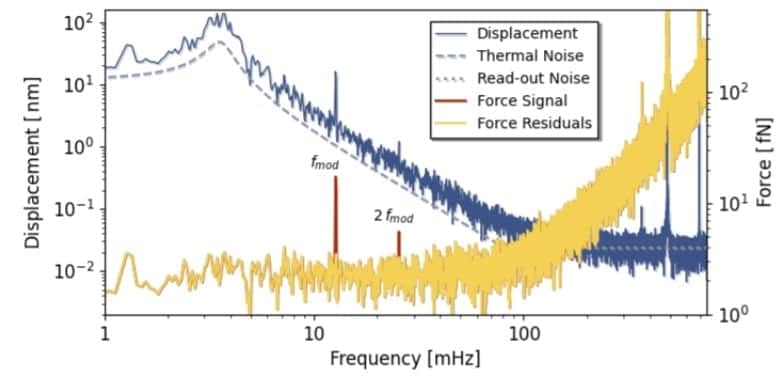
La détection d’un si minuscule signal gravitationnel est en soi un résultat passionnant, mais les auteurs sont allés encore plus loin en déterminant une valeur de G à partir de leur expérience. Leur estimation s’écarte d’environ 9% de la valeur convenue au niveau international — une petite quantité, étant donné que les incertitudes expérimentales de leur système n’ont pas encore été optimisées pour des mesures précises de G.

L’expérience est donc la première à montrer que la loi de la gravité de Newton est valable même pour des masses sources aussi petites que celles-ci. L’étape suivante consiste à atteindre des masses encore plus petites. Les chercheurs suggèrent que des champs gravitationnels de masses de l’ordre de 10^-8 kg pourraient éventuellement être mesurés.

Cependant, il reste encore beaucoup à faire pour atteindre cet objectif. La première tâche sera de réduire considérablement l’amortissement des oscillations de la balance de torsion, ce qui ne sera pas facile. Mais si cela peut être fait, alors peut-être que des effets gravitationnels quantiques seront finalement observés.

Sources : arXiv