Des chercheurs sont en train de mettre au point un algorithme quantique capable d’effectuer des calculs d’interaction de parallélisme de circuits quantiques et de configuration complète dans n’importe quelle molécule à couches ouvertes, sans explosion exponentielle ou combinatoire. Cela a déjà permis d’aboutir au premier exemple pratique d’algorithmes quantiques permettant de réaliser des calculs chimiques quantiques sur des ordinateurs quantiques équipés d’un grand nombre de qubits.
L’informatique quantique et la technologie de traitement de l’information quantique ont récemment attiré l’attention dans de nombreux domaines émergents. En effet, la résolution de l’équation de Schrödinger (dite ES) est l’un des objectifs ultimes de la chimie, de la physique et des domaines connexes, parmi de nombreux problèmes importants et fondamentaux de la science actuelle.
Cette équation, conçue par le physicien autrichien Erwin Schrödinger en 1925, est une équation fondamentale en mécanique quantique. Elle décrit l’évolution dans le temps d’une particule massive non relativiste, et remplit ainsi le même rôle que la relation fondamentale de la dynamique en mécanique classique. L’ES est le « premier principe » de la mécanique quantique non relativiste, dont les solutions, appelées fonctions d’onde, peuvent fournir n’importe quelle information d’électrons au sein d’atomes et de molécules, en prédisant leurs propriétés physicochimiques et leurs réactions chimiques.
À présent, des chercheurs de l’Université de la ville d’Osaka (OCU) au Japon, soit le Dr. K. Sugisaki, les professeurs K. Sato et T. Takui, ainsi que leurs collègues, ont découvert un algorithme quantique nous permettant d’effectuer des calculs d’interaction de configuration complète (dite IC complète) pour toutes les molécules à couches ouvertes, sans explosion exponentielle ou combinatoire.
Vous aimerez également : Sommes-nous des ordinateurs quantiques ?
L’interaction de configuration complète est une approche variationnelle linéaire qui fournit des solutions numériquement exactes (dans l’ensemble de base complet infiniment flexible) à l’équation électronique de Shrödinger. En effet, l’IC complète donne les solutions numériques exactes de l’ES, qui constitue l’un des problèmes insolubles pour tous les superordinateurs. Créer un tel algorithme quantique contribue donc fortement à l’accélération de la mise en œuvre des ordinateurs quantiques.
Les chercheurs expliquent : « Comme le disait Dirac en 1929, lors de l’établissement de la mécanique quantique, l’application exacte des théories mathématiques à la résolution de l’ES conduit à des équations trop compliquées pour être résolues. En fait, le nombre de variables à déterminer dans la méthode IC croît de manière exponentielle par rapport à la taille du système, et se heurte facilement à des chiffres astronomiques tels que l’explosion exponentielle ».
Selon le groupe de recherche de l’OCU, les ordinateurs quantiques peuvent remonter à la suggestion de Feynman datant de 1982, selon laquelle la mécanique quantique peut être simulée par un ordinateur lui-même construit à partir d’éléments de la mécanique quantique, et qui obéissent à des lois de la mécanique quantique.
C’est seulement plus de 20 ans plus tard que le professeur Aspuru-Guzik, de l’université Harvard et de la Toroto University (depuis 2018), et ses collègues, ont proposé un algorithme quantique capable de calculer les énergies des atomes et des molécules, non pas de façon exponentielle, mais de façon polynomiale par rapport au nombre de variables des systèmes, marquant une avancée décisive dans le domaine de la chimie quantique pour les ordinateurs quantiques.
Lorsque l’algorithme quantique d’Aspuru est appliqué aux calculs d’IC complète sur des ordinateurs quantiques, de bonnes fonctions d’onde approximatives proches des fonctions d’onde exactes de l’ES étudiée sont nécessaires : sinon, les fonctions d’onde nécessitent un nombre extrême d’étapes de calcul répétés pour atteindre les objectifs exacts, ce qui nuit clairement aux avantages de l’informatique quantique.
Ce problème devient donc extrêmement problématique pour tous les systèmes à couches ouvertes, dans lesquels de nombreux électrons non appariés ne participent pas à la liaison chimique.
Les chercheurs de l’OCU ont abordé ce problème, qui est l’un des problèmes les plus difficiles à résoudre en science quantique, et ont réalisé, en 2016, une avancée décisive dans la mise en œuvre d’un algorithme quantique générant des fonctions d’onde particulières appelées fonctions d’état de configuration dans le temps de calcul polynomial.
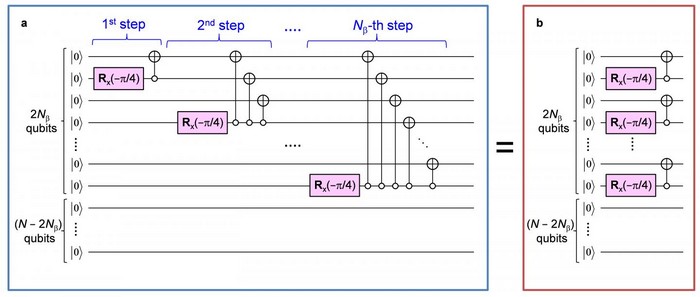
Cependant, l’algorithme précédemment proposé nécessite un nombre considérable d’opérations de porte de circuit quantique proportionnelles aux carrés du nombre de N, ce qui correspond au nombre de descentes des électrons non appariés dans le système. Ainsi, si N augmente, le temps de calcul total n’augmente pas de façon exponentielle, mais de manière drastique tout de même.
De plus, la complexité des circuits quantiques devrait être réduite pour une utilisation pratique de l’algorithme et de l’architecture de programmation quantique. À savoir qu’il existe un nouvel algorithme quantique qui exploite les fonctions de spin germinal, appelé construction de Serber, et qui réduit le nombre d’opérations de porte à seulement 2N, exécutant le parallélisme des portes quantiques.
« C’est le premier exemple pratique d’algorithmes quantiques permettant de réaliser des calculs chimiques quantiques sur des ordinateurs quantiques équipés d’un nombre considérable de qubits. Ces implémentations permettent des applications pratiques des calculs chimiques quantiques sur ordinateurs quantiques, dans de nombreux domaines importants », a expliqué le groupe de recherche de l’OCU.
L’électron est une particule élémentaire qui, avec les protons et
les neutrons, constitue les atomes. C’est donc l’un des composants
principaux de la matière baryonique. À ce titre, il revêt... [...]