Si vous avez déjà observé attentivement des bulles de savon, vous avez sans doute constaté qu’elles tendent à s’agglutiner. Elles forment spontanément des amas de façon à minimiser la surface totale de leurs parois (y compris les interfaces qui séparent chaque bulle). L’an dernier, deux mathématiciens — Emanuel Milman, du Technion et Joe Neeman, de l’Université du Texas, à Austin — ont prouvé pour la première fois que la triple bulle était la forme de moindre surface permettant d’enfermer trois volumes séparés.
En raison de la tension superficielle, les bulles de savon (ou les amas de bulles) essaient naturellement de minimiser la surface du ou des volumes qu’elles renferment. Ceci constitue un problème mathématique célèbre, dit « des bulles de savon » : comment contenir et séparer n volumes d’air en utilisant le moins de surface possible ? En 1884, le mathématicien allemand Hermann Schwarz a prouvé qu’une sphère (telle qu’une bulle de savon par exemple) a une surface inférieure à celle de tout autre corps de même volume.
Ce n’est que plus d’un siècle plus tard, en 2000, que Michael Hutchings, Frank Morgan, Manual Ritoré et Antonio Ros ont prouvé que la double bulle de savon — qui se forme spontanément lorsque deux bulles de savon se rencontrent — est la meilleure façon de minimiser la surface de deux volumes séparés. Pour davantage de volumes, le problème se complique. Il faut envisager un très large éventail de formes possibles, voire envisager de subdiviser l’un des volumes en plusieurs volumes plus petits. L’an dernier, Emanuel Milman et Joe Neeman ont toutefois réussi à prouver la conjecture de la triple bulle.
Un seul et unique amas de moindre surface
Si, dans la nature, les amas de bulles tendent à adopter la configuration de moindre énergie, il n’était pas certain que cette observation se vérifie d’un point de vue mathématique. Dans les années 1990, John Sullivan — aujourd’hui chercheur à l’Université technique de Berlin — a montré que lorsque le nombre de volumes que l’on souhaite enfermer est au maximum supérieur d’une unité à la dimension considérée, il existe un seul et unique amas qui semble surpasser tous les autres (en matière de minimisation de surface). Cette conjecture permet de considérer des groupes de trois bulles dans l’espace bidimensionnel, de quatre bulles dans l’espace tridimensionnel, de cinq bulles dans l’espace quadridimensionnel, etc.
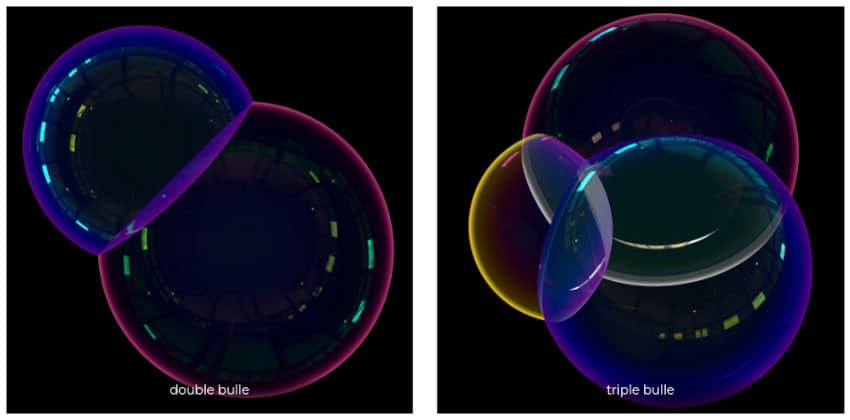
Milman et Neeman ont utilisé l’approche de Sullivan pour résoudre le problème de la triple bulle. Ils ont ainsi prouvé que la triple bulle standard, composée de calottes sphériques se rencontrant à 120 degrés le long d’arcs de cercle, qui se rencontrent à leur tour à des angles d’environ 109° (tel l’angle central d’un tétraèdre régulier), est la façon la plus simple d’entourer et de séparer trois volumes donnés, voire plus encore.
Dans la nature, les bulles ont des parois sphériques ou planes et lorsque trois parois se rencontrent, elles forment des angles de 120°. Chacun des volumes se trouve dans une seule région (ils ne sont donc pas divisés). Et chaque bulle touche toutes les autres, formant ainsi une grappe serrée. Les deux mathématiciens ont montré que les bulles de Sullivan sont les seuls amas qui satisfont à toutes ces propriétés. Jusqu’à présent, la conjecture des bulles triples n’avait été prouvée que dans le plan bidimensionnel, où les interfaces entre les bulles sont les plus simples, souligne Quanta Magazine.
Un principe qui n’est pas (encore) généralisable
Dans un premier temps, les deux mathématiciens ont ajouté une dimension supplémentaire à leur amas de bulles, pour faciliter leurs calculs ; le « meilleur » amas présentait dans ce cas une symétrie miroir par rapport à un plan central. Cette symétrie « bonus » leur a permis de trouver un « argument de perturbation », qui consiste à gonfler légèrement la moitié de l’amas de bulles qui se trouve au-dessus du miroir et à dégonfler la moitié qui se trouve en dessous. Cette perturbation ne changeait pas le volume total des bulles, mais pouvait modifier leur surface.
Ils ont alors montré que si la grappe de bulles optimale possède des parois qui ne sont pas sphériques ou plates, il est possible de choisir cette perturbation de manière à ce qu’elle réduise la surface totale. Ils ont ainsi utilisé ces perturbations pour montrer que la grappe de bulles optimale doit satisfaire à toutes les caractéristiques essentielles des grappes de Sullivan, à l’exception du fait que chaque bulle doit toucher toutes les autres.
Cette exigence a obligé les deux mathématiciens à envisager toutes les façons dont les bulles pouvaient s’agglutiner. Avec trois ou quatre bulles, la liste des possibilités est relativement restreinte, mais plus le nombre de bulles augmente, plus le nombre de possibilités augmente de manière exponentielle.
Bien qu’ils espéraient trouver un principe général permettant d’expliquer tous les cas, leur approche ne concerne que les bulles triples et quadruples. Ils ont également annoncé avoir trouvé la preuve que la bulle quintuple de Sullivan est optimale, mais ils n’ont pas encore pu établir qu’il s’agissait du seul arrangement optimal possible.

