L’intrication quantique pourrait en réalité posséder une distance maximale

En d’autres termes, pour des seuils d’énergies élevés, la QFT est insuffisante et présente des défauts. Pour des niveaux d’énergie élevés, la QFT doit être renormalisée, c’est-à-dire qu’elle présente des quantités infinies qui doivent être corrigées. Et pour des niveaux ultra-énergétiques, les champs quantiques génèrent leurs propres champs gravitationnels, qui ne peuvent être ignorés ; cependant, aucune théorie de la gravité quantique n’est actuellement capable de prendre en charge ce « problème ».

Parallèlement, la QFT devient également problématique sur les très grandes distances. À de grandes échelles, la valeur de l’énergie du vide quantique, estimée par le calcul comme étant de 10¹¹³ J/m³, est déterminée expérimentalement à 10^-9 J/m³. Les valeurs théorique et expérimentale divergent donc de l’ordre d’un facteur 10¹²⁰ ; cette divergence, appelée « catastrophe du vide », demeure inexpliquée.

Cette inapplicabilité de la QFT sur de très grandes distances n’est pas nouvelle et a déjà fait l’objet de démonstrations théoriques dans de précédentes études. Pour ce faire, des physiciens ont notamment établi une relation entre les seuils d’énergie ultraviolet (UV) « Λ » et infrarouge (IR) « ħ/L » du Modèle Standard (3) : L ≤ m_p/Λ², avec « mp » la masse de Planck.

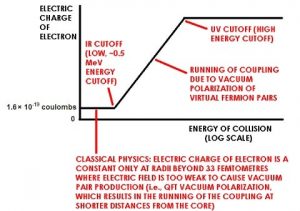
Ainsi, lorsque cette relation est appliquée à l’échelle de l’horizon cosmologique, le seuil d’énergie d’UV correspondant est de Λ ~ 10^-2.5 eV. Grâce à cette relation UV-IR, les chercheurs peuvent démontrer que pour des valeurs de Λ > 10^-2.5 eV, donc sur des distances extrêmement grandes, la QFT cesse de fonctionner correctement. Dès lors, puisque l’intrication quantique découle de la QFT, elle aussi doit être spatialement limitée.

Dans sa publication, et en se basant sur ces précédents travaux, Y. Xiao réécrit la relation UV-IR pour la faire correspondre à une distance maximale de l’intrication quantique et obtient la relation : L_QE ≤ λ²/lp, avec « L_QE » la longueur de l’intrication, « λ » la longueur d’onde quantique des particules intriquées et « lp » la longueur de Planck.

Suivant cette relation, les particules satisfaisant la condition Λ ≤ 10^-2.5 eV (c’est-à-dire une longueur d’onde λ ≥ 4×10^-4 m) peuvent être intriquées de manière stable sur des distances de l’ordre de l’horizon cosmologique. À l’opposé, les particules pour lesquelles Λ > 10^-2.5 eV (longueurs d’ondes courtes) voient leur relation d’intrication se rompre à l’échelle cosmologique, en raison des perturbations quantiques gravitationnelles.

Situation dans laquelle α = 3 : information et principe holographique

Initialement proposé par Gerard ‘t Hooft en 1993 puis développé par Leonard Susskind, le principe holographique énonce que la quantité maximale d’information contenue dans un volume d’espace ne peut être supérieure à celle emmagasinée à la surface de ce volume. En d’autres termes, l’information contenue dans un volume d’espace est encodée, stockée sur sa surface. Ainsi, l’entropie maximum à l’intérieur d’un volume est égale à A/lp^2, où « A » est l’aire de la surface (en unités de Planck).

Dans leurs travaux, les mêmes physiciens ayant proposé la relation UV-IR, L ≤ mp/Λ², ont également construit une seconde relation UV-IR mais cette fois-ci basée sur le principe holographique et s’écrivant : L ≤ mp²/Λ³ (3). Dans le même objectif, l’auteur traduit cette relation en terme de distance maximale pour l’intrication quantique : L_QE ≤ λ³/lp².

Cette relation est, selon l’auteur, certainement plus correcte que celle s’appuyant sur α = 2. Le principe holographique est, en effet, très fortement corrélé à la notion d’information, puisqu’il définit la quantité maximale d’information que peut posséder un système. De la même manière, l’intrication quantique est aussi un phénomène intimement relié à l’information. Il apparaît donc naturel que principe holographique et intrication quantique soient liés.

Selon cette relation, une distance infinie pour l’intrication quantique est incompatible avec le principe holographique. Pour le démontrer, prenons l’hypothèse d’une distance effectivement infinie et considérons une paire de particules intriquées. Si l’on mesure l’une des deux particules seule, l’entropie de Von Neumann (entropie de Gibbs appliquée à la mécanique quantique) est égale à S = ln 2.

Par la suite, l’on considère plusieurs paires intriquées et l’on place une particule de chaque paire dans une boîte de rayon R et l’autre très loin à l’extérieur de la boîte. L’on peut accumuler au maximum N = R³/λ³ dans cette dernière. L’entropie de Von Neumann de la boîte est alors S = N ln 2. Ainsi, pour des longueurs d’onde suffisamment courtes, l’entropie (S) est supérieure à A/lp² et le principe holographique est alors violé.

Maintenant, considérons l’hypothèse pour laquelle l’intrication quantique possède une distance maximale L_QE = λ³/lp². La boîte contient un nombre N = R³/λ³ de particules. Pour des longueurs d’onde λ > R^1/3lp^2/3, la distance maximale d’intrication L_QE est supérieure au rayon R de la boîte, l’intrication quantique de toutes les paires est donc maintenue, et l’entropie de la boîte (S) est inférieure ou égale à A/lp², ce qui respecte le principe holographique.

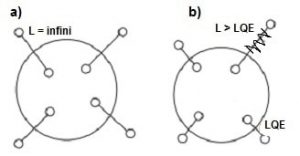
Dans le cas de longueurs d’onde courtes, c’est-à-dire λ < R^1/3lp^2/3, l’intrication quantique est rompue et la particule à l’intérieur de la boîte retourne à un état non-intriqué. Dès lors, elle ne participe plus à l’entropie totale de la boîte. Donc seule une certaine partie des particules pour lesquelles L_QE ≤ λ³/lp² participe à l’entropie de cette dernière, de telle sorte que l’entropie reste S = A/lp² ln 2, en accord avec le principe holographique.

En résumé : dans l’hypothèse où l’intrication possède une distance infinie, l’entropie que possède une particule intriquée occupant un volume d’espace est supérieure à l’entropie contenue sur la surface de ce volume, violant ainsi le principe holographique. À l’opposé, dans l’hypothèse d’une distance maximale d’intrication L_QE, l’intrication se rompt au-delà de cette distance, dès lors la particule désintriquée ne participe plus à l’entropie du volume d’espace, qui reste inférieure ou égale à l’entropie de la surface de ce volume, en accord avec le principe holographique.

Les conditions expérimentales d’observation d’une distance maximale d’intrication

La distance maximale d’intrication étant liée à l’existence d’effets quantiques gravitationnels perturbatifs, cela rend le phénomène extrêmement complexe à observer. Ainsi, pour des photons d’une longueur d’onde de 800 nm (tels que ceux émis par le satellite Micius), la distance maximale d’intrication L_QE peut être supérieure à 10²² m si α = 2 et à 10⁵¹ m si α = 3.

En utilisant les deux relations précédemment données pour L_QE, pour observer une rupture de l’intrication quantique sur une distance de 1200 km, cela nécessiterait d’utiliser des photons possédant une énergie de 10 MeV, voire 100 TeV, en fonction de la valeur du coefficient α. De tels distances et de tels seuils d’énergie sont pour le moment inaccessibles à l’expérimentation.

Sources : Arxiv.org (1, 2, 3)