Des chercheurs ont identifié une corrélation entre la théorie des nombres et la génétique évolutive, suggérant que des principes mathématiques purs pourraient influencer la biologie. Cette découverte, basée sur la robustesse phénotypique, révèle que les génotypes pourraient être organisés selon des motifs mathématiques. Cette perspective offre une nouvelle dimension à la recherche, indiquant que les mathématiques pures pourraient être plus intrinsèquement liées à la vie qu’on ne le pensait.
La fusion entre les mathématiques et la biologie a toujours été une source d’interrogations et d’explorations pour les chercheurs. Un domaine particulier a été récemment mis en lumière concernant l’évolution. Des chercheurs de la Royal Society se sont intéressés à la robustesse phénotypique. Il s’agit de la robustesse mutationnelle moyenne de tous les génotypes associés à un phénotype donné. Elle est essentielle pour comprendre les mécanismes sous-jacents à l’apparition de nouvelles variations phénotypiques dans une population en évolution.
Les auteurs suggèrent que la nature elle-même pourrait être régie par des principes mathématiques purs, une connexion surprenante entre la théorie des nombres et la génétique évolutive. Les travaux sont publiés dans la revue Journal of The Royal Society Interface.
Quand la théorie des nombres rencontre la biologie
La théorie des nombres, traditionnellement associée à des domaines purement mathématiques, a trouvé une application surprenante dans la biologie évolutive. Les chercheurs ont utilisé cette théorie pour étudier la robustesse phénotypique, une caractéristique essentielle pour comprendre comment les organismes évoluent face aux mutations. Ils ont découvert que cette robustesse atteint son apogée lorsque les génotypes, qui sont les codes génétiques d’un organisme, sont structurés selon un modèle particulier appelé « graphes maçon » (« Bricklayer’s graphs »). Ce nom vient du fait qu’ils sont construits par l’ajout répété d’un sommet adjacent dans le graphe de Hamming (un concept mathématique utilisé pour mesurer les distances entre les séquences de codes), évoquant le processus de pose de briques.
Mais ce qui est encore plus fascinant, c’est que la valeur maximale de cette robustesse phénotypique est déterminée par une fonction mathématique très spécifique. Cette fonction est fractale, ce qui signifie qu’elle présente des motifs répétitifs à différentes échelles. Elle est continue, donc sans interruptions, mais elle présente une particularité : elle n’est différentiable en aucun point. En d’autres termes, elle est si complexe et irrégulière qu’on ne peut pas calculer sa pente en un point donné. Cette fonction, bien qu’elle provienne de la théorie des nombres, pourrait être la clé pour comprendre comment la nature a optimisé la capacité des organismes à évoluer et à s’adapter à leur environnement.
Des implications profondes pour la biologie
Le professeur Ard Louis de l’Université d’Oxford, qui a dirigé l’étude, explique dans un communiqué : « Nous savons depuis un certain temps que de nombreux systèmes biologiques présentent une robustesse phénotypique remarquablement élevée, sans laquelle l’évolution ne serait pas possible ». Mais les scientifiques ne savaient pas quelle serait la robustesse maximale absolue, ni même s’il existait un maximum. C’est précisément à cette question que l’équipe a répondu.
Pour ce faire, les chercheurs se sont appuyés sur les cartes génotype-phénotype. Ce sont des outils essentiels en biologie qui permettent de comprendre comment les variations génétiques (génotypes) se traduisent en caractéristiques observables (phénotypes). En particulier, la structure secondaire de l’ARN est une configuration spatiale de l’ARN qui joue un rôle crucial dans son fonctionnement et sa régulation. De même, le repliement des protéines, gouverné par le modèle hydrophobe-polaire (HP), détermine la forme tridimensionnelle des protéines, essentielle à leur fonction.
Lorsque l’on examine ces cartes pour la structure secondaire de l’ARN et le modèle HP, on constate qu’elles peuvent afficher une robustesse phénotypique qui atteint la limite supérieure définie par les principes mathématiques mentionnés précédemment.
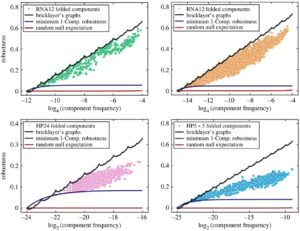
Ils ont alors prouvé que la robustesse maximale est proportionnelle au logarithme de la fraction de toutes les séquences possibles correspondant à un phénotype, avec une correction qui est donnée par la fonction de somme des chiffres sk(n), définie comme la somme des chiffres d’un nombre naturel n en base k. Par exemple, pour n = 123 en base 10, la somme des chiffres serait s10(123) = 1 + 2 + 3 = 6.
L’auteur principal, le Dr Vaibhav Mohanty (Harvard Medical School), déclare : « Le plus surprenant est que nous avons trouvé des preuves claires dans la cartographie des séquences aux structures secondaires d’ARN que la nature atteint dans certains cas la limite de robustesse maximale exacte ».
Un avenir prometteur pour la recherche
Ce constat suggère que la nature, dans sa quête d’optimisation, pourrait avoir adopté des configurations génétiques qui correspondent à des modèles mathématiques précis. Autrement dit, les principes mathématiques ne seraient pas de simples outils d’analyse, mais pourraient être intrinsèquement liés à la manière dont la vie évolue et s’adapte. Cela offre une nouvelle perspective sur notre compréhension traditionnelle de la biologie évolutive, suggérant que les mathématiques pourraient être au cœur même des mécanismes de l’évolution.
Cette fusion de la biologie et des mathématiques ouvre la voie à de nouvelles méthodes de recherche et à une meilleure compréhension de l’évolution. En reconnaissant les motifs mathématiques sous-jacents dans la génétique, les scientifiques peuvent désormais envisager de nouvelles approches pour étudier et peut-être même influencer l’évolution.


