Les équations aux dérivées partielles, aussi appelées équations différentielles partielles, ou EDP, sont une catégorie d’équations mathématiques qui peuvent décrire absolument tous les phénomènes physiques de notre univers : des orbites planétaires à la tectonique des plaques, en passant par les turbulences de l’air susceptibles de perturber un vol. Ces équations très complexes et particulièrement difficiles à résoudre sont généralement prises en charge par des supercalculateurs. Des chercheurs de Caltech proposent aujourd’hui une nouvelle technique pour résoudre ces EDP, basée sur l’apprentissage profond.
Parce qu’elles peuvent être utilisées pour modéliser tous les changements observables dans l’espace et le temps, les EDP sont largement utilisées pour anticiper de nombreux phénomènes, comme les courants océaniques, l’activité sismique, le mouvement des masses d’air, le comportement des ponts et gratte-ciels sous l’action du vent, etc. La résolution de ces EDP est donc primordiale dans des domaines tels que la météorologie ou l’aéronautique, entre autres.
Un calcul de haute précision en un temps record
Les équations de Navier-Stokes, par exemple, sont des EDP qui permettent de décrire le mouvement d’un fluide. Elles sont notamment utilisées en aéronautique pour simuler les turbulences de l’air et tester le comportement d’un nouveau concept d’avion. Résoudre ces équations consiste à considérer un instantané du mouvement de l’air (soit les conditions de vent à un instant t) et à modéliser ses déplacements passés et futurs. Les supercalculateurs s’en sortent généralement très bien, mais l’usage de l’apprentissage profond (ou deep learning) permettrait d’accélérer encore le processus de résolution.
Des chercheurs de Caltech ont réfléchi à la question et proposent aujourd’hui une nouvelle technique pour résoudre les EDP, beaucoup plus précise que les méthodes d’apprentissage profond développées précédemment. Leur méthode présente également l’avantage d’être généralisable, autrement dit, elle est capable de résoudre des familles entières d’EDP sans nécessiter de nouvel entraînement. Enfin, elle s’avère 1000 fois plus rapide que les formules mathématiques traditionnelles, ce qui augmenterait la capacité de calcul et donc, permettrait de modéliser des problèmes encore plus complexes.
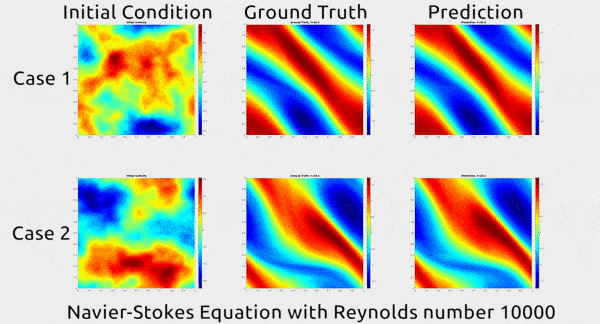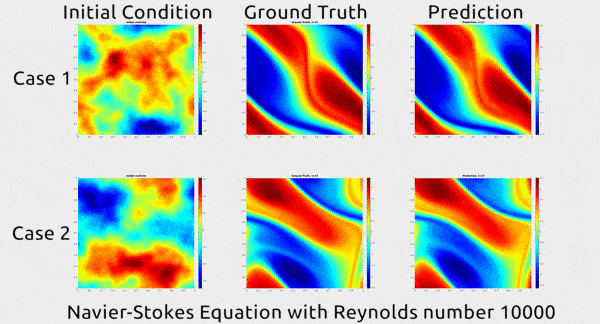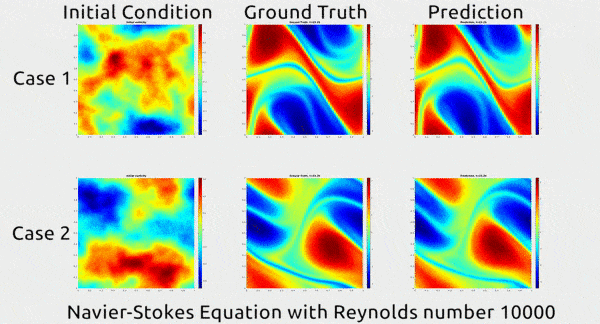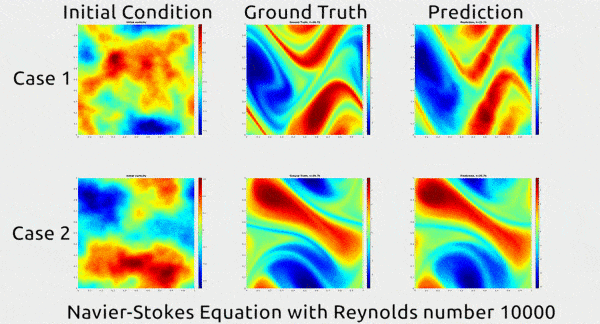
À titre d’exemple, les chercheurs ont soumis une équation de Navier-Stokes à leur algorithme de calcul (avec 10’000 comme nombre de Reynolds, une variable correspondant au rapport entre les forces d’inertie et les forces visqueuses, qui caractérise l’écoulement du fluide). Ils ont publié une animation montrant comment le fluide a continué à se déplacer dans la vie réelle et comment leur réseau neuronal a prédit que le fluide se déplacerait. Les résultats sont impressionnants de similitude :
En quoi consiste la technique d’apprentissage profond développée par ces chercheurs ? La première chose à comprendre est que les réseaux de neurones sont fondamentalement des approximateurs de fonctions : lorsqu’ils s’entraînent sur un ensemble de données d’entrées et de sorties appariées, ils calculent en fait la meilleure fonction qui permet de passer de l’une à l’autre. Dans le cas d’une EDP, il s’agit de trouver une fonction qui décrit le mieux, par exemple, le mouvement des particules d’air dans l’espace physique et dans le temps.
Les réseaux de neurones sont généralement formés pour approximer les fonctions entre les entrées et les sorties définies dans l’espace euclidien (soit une représentation classique de l’espace, avec les axes x, y et z). Or, cette fois-ci, les chercheurs ont décidé de définir les entrées et les sorties dans l’espace de Fourier, un type de représentation généralement utilisé pour tracer les fréquences d’onde.
Des prévisions météorologiques à l’échelle mondiale
Anima Anandkumar, une professeure de Caltech qui a supervisé la recherche, explique que cette idée leur est venue du fait que le mouvement de l’air peut en fait être décrit comme une combinaison de fréquences d’ondes : au niveau macroscopique, la direction globale du vent est comme une basse fréquence avec des ondes très longues et léthargiques, tandis que les petits tourbillons qui se forment au niveau microscopique sont comme de hautes fréquences, avec des ondes très courtes et rapides.
L’utilisation de l’espace de Fourier simplifie grandement le travail du réseau neuronal. En plus d’être beaucoup plus rapide que les méthodes traditionnelles, cette nouvelle technique atteint un taux d’erreur 30% inférieur à celui obtenu via les méthodes de deep learning précédentes lors de la résolution d’équations de Navier-Stokes. Cerise sur le gâteau : alors que les anciennes méthodes devaient être entraînées séparément (un entraînement pour chaque type de fluide), ce nouvel algorithme d’apprentissage n’a besoin d’être formé qu’une seule fois pour les gérer tous !
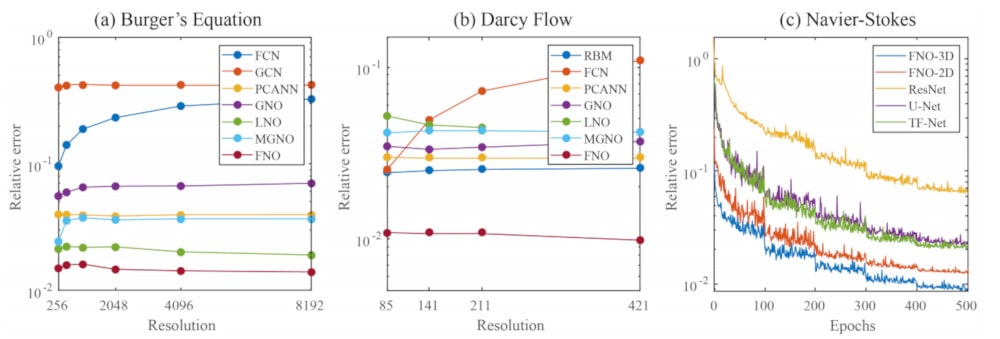
Concernant les équations de Navier-Stokes, la technique est donc applicable pour n’importe quel fluide. Les chercheurs n’ont pas encore eu l’occasion d’expérimenter leur méthode de calcul sur d’autres types d’équations, mais elle devrait par exemple être capable de gérer n’importe quelle composition du sol lors de la résolution d’EDP liées à l’activité sismique, ou n’importe quel type de matériau pour les EDP liées à la conductivité thermique.
C’est en discutant avec divers collaborateurs en sciences du climat, en sismologie et en sciences des matériaux qu’Anandkumar a décidé pour la première fois de relever le défi des EDP. La spécialiste en IA s’intéresse en particulier aux modélisations météorologiques, dans le cadre de l’étude du changement climatique, un domaine dans lequel les équations de Navier-Stokes sont incontournables : « Avoir de bonnes prévisions météorologiques précises à l’échelle mondiale est un problème tellement difficile… Même sur les plus gros supercalculateurs, nous ne pouvons pas le faire à l’échelle mondiale aujourd’hui. Donc, si nous pouvons utiliser ces méthodes pour accélérer l’ensemble du pipeline, cela aura un impact énorme », dit-elle.
Ses collaborateurs et elle travaillent maintenant à mettre leur méthode en pratique avec d’autres chercheurs de Caltech et du Lawrence Berkeley National Laboratory, pour mettre cette intelligence artificielle à profit dans d’autres disciplines scientifiques.