Cependant, c’est au satellite Microscope que l’on doit depuis le 4 décembre 2017 les mesures les plus précises jamais réalisées. En effet, les scientifiques sont parvenus à une précision inégalée de 2×10-14 g, soit cent fois plus de précision que les dernières mesures réalisées sur Terre.
Pour ce faire, le satellite a emporté deux paires de cylindres coulissants, l’une en platine et l’autre en titane pour le cylindre extérieur. En l’absence de frottements dus à l’air et en accord avec le principe d’équivalence, les deux masses, de compositions chimiques différentes, devraient rester immobiles l’une par rapport à l’autre ; en d’autres termes, l’accélération subie par les deux masses devraient être identique et celles-ci devraient donc chuter de la même manière.
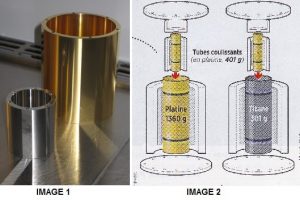
Afin de maintenir des conditions de mesure optimales, Microscope intègre un système de compensation de traînée par poussées afin de corriger les forces extérieures (photons solaires, molécules atmosphériques…) qui impactent la chute libre. Car c’est en cela que réside tout l’intérêt de l’expérience : étant en orbite autour de la Terre, le satellite conserve une chute libre permanente idéale pour l’expérimentation.
En outre, Microscope embarque un accéléromètre pouvant mesurer une accélération de 8×10-15 m/s2. Cette ultrasensibilité de détection lui permet ainsi d’être tout à fait en mesure de détecter la moindre violation du principe d’équivalence. Selon Pierre-Yves Guidotti (chef de projet exploitation), avec une telle accélération, il faudrait 5 millions d’années pour atteindre la vitesse de marche d’un piéton.
Les scientifiques ont ainsi analysés les résultats de mesure de 120 orbites sur les 1900 réalisées, soit seulement 10% des données acquises. Cependant, ces résultats ont été suffisants pour confirmer le principe d’équivalence avec une précision extrême de 2×10-14 g. Cent ans après la publication de ses travaux, il s’avère qu’Einstein a, une nouvelle fois, raison.
Mais la mission de Microscope ne s’arrête pas ici. Le satellite est conçu pour continuer ses mesures jusqu’en mars 2018. Les données ainsi recueillies permettront aux scientifiques d’atteindre une précision de 10-15 g ; un seuil qui, peut-être, permettra de mettre en défaut les prédictions de la relativité générale.
Pour quelles raisons tester le principe d’équivalence ?
La question est légitime : si le principe d’équivalence est confirmé par l’expérience depuis des dizaines d’années, pourquoi continuer à le tester ? Tout d’abord, si le principe d’équivalence est accepté et connu de tous, pour les physiciens, paradoxalement, aucune raison ne le justifie. Pourtant, nous l’observons en permanence.
Selon le physicien Thibault Damour, si le principe d’équivalence est pour le moment vérifié aux échelles de précision qui nous sont accessibles, ce n’est peut-être pas le cas pour des échelles plus précises.
Et observer une violation du principe d’équivalence ne serait pas sans conséquences. Cela indiquerait que, bien que la relativité générale soit une théorie élégante et solide, celle-ci serait incomplète et nécessiterait d’être corrigée afin de correspondre plus fidèlement à la dynamique de l’univers.
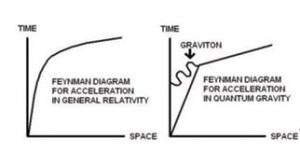
En outre, si la relativité générale offre une description précise de l’univers sur les grandes échelles, son application aux échelles microscopiques représente un des obstacles et enjeux les plus importants de la physique moderne. En effet, à de telles échelles, la relativité générale doit s’accommoder de la mécanique quantique à travers une théorie unificatrice appelée « théorie de la gravité quantique ».
Or, une grande partie des théories à gravité quantique actuellement en développement prédisent justement une violation du principe d’équivalence (4). Parmi ces théories, la théorie des cordes propose un mécanisme à l’origine de cette violation par l’intermédiaire d’une particule hypothétique émergeant simultanément avec le graviton : le dilaton. Le modèle du dilaton a été introduit par les physiciens cordistes C. Callan, S. Giddings, J. Harvey et A. Strominger.
Le dilaton est une particule agissant de manière synchrone avec l’interaction gravitationnelle, son effet s’ajoutant à cette dernière (5). Là où le graviton (la gravitation) agit sur la masse de l’objet, le dilaton agit sur l’interaction électromagnétique régnant au sein du noyau atomique. L’intensité du dilaton varie donc en fonction de la composition chimique de l’objet. La résultante graviton+dilaton n’est donc pas la même en fonction de l’objet considéré (6).


Fortement couplée à la matière dans les premiers instants de l’univers, « l’interaction dilatonique » a progressivement diminué jusqu’à devenir aujourd’hui extrêmement faible. Elle n’a cependant pas disparu selon les physiciens T. Damour, F. Piazza et G. Veneziano. Le dilaton continue de se coupler de manière très faible à la matière et, à de très petites échelles, pourrait être responsable de la violation du principe d’équivalence (7).
De la même manière, la théorie de la gravitation quantique à boucles prédit elle aussi une violation du principe d’équivalence (4). Dans le cadre de cette théorie, certaines constantes fondamentales varient en fonction de l’existence de divers champs scalaires, impactant directement la dynamique des objets en fonction de leur structure.
Toutefois, de récentes études ont montré que de telles violations du principe d’équivalence, indifféremment de la théorie considérée, ne peuvent être perçues qu’à des échelles de précision comprises entre 10-15 et 10-18 g. Avec les futures données acquises par Microscope, les chercheurs espèrent avoir la surprise de découvrir qu’Einstein n’avait, finalement, peut être pas raison sur toute la ligne.


