Dans la plupart des situations de la vie quotidienne, les systèmes de calcul numérique que nous utilisons sont amplement suffisants en matière de précision. Mais lorsque les scientifiques ont besoin d’effectuer des simulations et des calculs complexes, la précision numérique est d’une importance primordiale. Toutefois, dans une nouvelle étude, des chercheurs ont découvert que les calculs complexes effectués par ordinateur pouvaient être biaisés jusqu’à 15%, en raison d’une incapacité pathologique à saisir la véritable complexité mathématique des systèmes dynamiques chaotiques.
« Notre travail montre que le comportement des systèmes dynamiques chaotiques est plus riche que tout ordinateur numérique peut en capturer » déclare l’informaticien Peter Coveney de l’UCL au Royaume-Uni. « Le chaos est plus banal que beaucoup de gens ne le pensent et même pour des systèmes chaotiques très simples, les nombres utilisés par les ordinateurs numériques peuvent entraîner des erreurs qui ne sont pas évidentes mais qui peuvent avoir un impact important ».
Pendant des siècles, les théoriciens ont envisagé comment de très petits effets en amont peuvent s’accumuler pour devenir très importants en aval. Dans la théorie du chaos, le phénomène est connu sous le nom d’effet papillon : métaphoriquement, la notion hypothétique selon laquelle le battement infiniment petit des ailes d’un papillon à un endroit pourrait aider à générer une tornade à un autre. Les résultats de l’étude ont été publiés dans la revue Advanced Theory and Simulations.
Chaos mathématique : l’extrême importance des conditions initiales
C’est un concept poétique, mais bien que cela puisse sembler fantaisiste, la modélisation mathématique suggère que la notion est ancrée dans des termes très mesurables. L’effet papillon est principalement attribué au mathématicien et météorologue américain Edward Norton Lorenz, qui, dans les années 1960, en répétant une simulation météorologique, a utilisé un raccourci mathématique qui façonnera l’histoire : il utilisa des nombres légèrement simplifiés pour la deuxième expérience (0.506 au lieu de 0.506127).
« Je suis allé prendre une tasse de café dans le couloir et je suis rentré au bout d’environ une heure, période pendant laquelle l’ordinateur avait simulé environ deux mois de météo. Les chiffres en cours d’impression ne ressemblaient en rien aux anciens » explique Lorenz.
Les résultats de l’arrondissement de Lorenz ont montré comment des changements minimes dans les conditions initiales peuvent produire de grands changements au fil du temps dans des systèmes complexes et chaotiques, dans lesquels de nombreuses variables s’affectent et s’influencent mutuellement.
Chaos et calculs complexes : l’effet boule de neige des erreurs d’imprécision
La prévision météorologique en est un exemple, mais le même phénomène d’erreurs en boule de neige a depuis été mis en évidence dans de nombreux domaines, de la modélisation des trajectoires orbitales à la turbulence et à la dynamique moléculaire. Le fait est que, même si l’effet papillon est connu depuis des décennies, il reste un problème fondamental dans la façon dont les ordinateurs exécutent les calculs.
Sur le même sujet : Pour la première fois, des scientifiques démontrent comment les systèmes chaotiques se synchronisent
« La sensibilité extrême aux conditions initiales est une caractéristique déterminante des systèmes dynamiques chaotiques. Depuis la première utilisation des calculateurs numériques pour la science informatique, il est connu que la perte de précision due à l’approximation discrète de nombres réels peut considérablement altérer la dynamique des systèmes chaotiques après une courte période de simulation » expliquent les chercheurs.
Cette perte de précision ne se manifeste pas dans les calculs simples. L’application calculatrice de votre smartphone est probablement parfaitement suffisante pour tout ce dont vous avez besoin dans la vie quotidienne. Mais dans les calculs complexes avec beaucoup de variables et de conditions de départ, de petites erreurs d’arrondi au début peuvent entraîner d’énormes erreurs de calcul à la fin d’une simulation donnée.
Le problème de l’utilisation des virgules flottantes
Les chercheurs expliquent que le cœur du problème est ce qu’on appelle l’arithmétique en virgule flottante : la manière standardisée de comprendre les nombres réels par des ordinateurs utilisant un code binaire, qui utilise des approximations et des conversions pour représenter des nombres.
Dans les systèmes vastes et complexes, ces approximations peuvent générer des erreurs significatives, un problème aggravé par la manière dont les nombres à virgule flottante sont répartis entre des nombres réels, même dans un format 64 bits plus récent et plus complexe appelé virgule flottante à double précision.
« On a longtemps pensé que les erreurs d’arrondi ne posaient pas de problèmes, en particulier si nous utilisions des nombres à virgule flottante à double précision — des nombres binaires utilisant 64 bits au lieu de 32. Mais dans notre étude, nous avons mis en évidence un problème dû à la distribution inégale des fractions représentées par les nombres à virgule flottante, et qui ne risque pas de disparaître simplement en augmentant le nombre de bits » explique le mathématicien Bruce Boghosian, de l’Université Tufts.
Une accumulation d’erreurs, y compris dans les calculs les plus simples
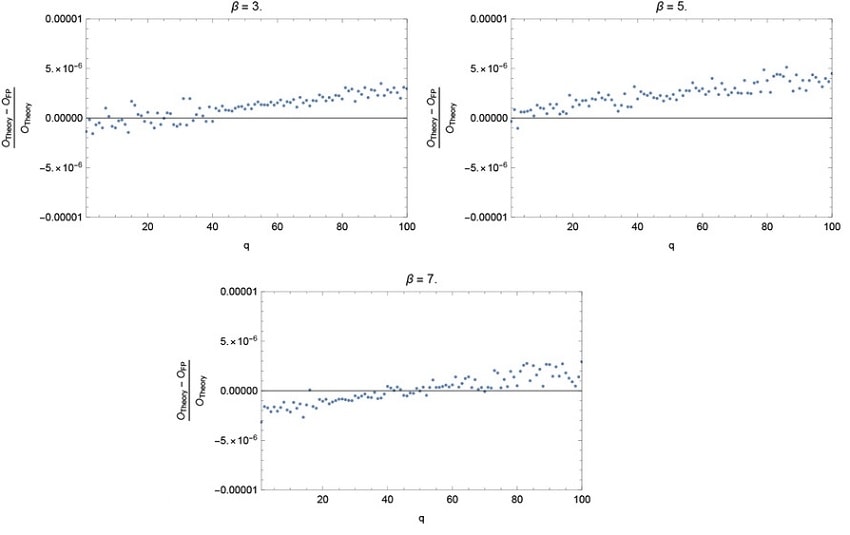
Dans le cadre de la recherche, l’équipe a comparé un système chaotique connu appelé carte de Bernoulli à un calcul numérique du même système et a découvert ce qu’elle qualifie de distorsions systématiques et de pathologies dans la simulation de systèmes dynamiques chaotiques. En effet, alors que Lorenz découvrait son effet papillon en laissant des chiffres entiers dans un calcul, les chercheurs trouvèrent leur propre équivalent beaucoup plus subtil en demandant simplement à un ordinateur de réaliser un calcul mathématique.
« Pour Lorenz, c’est un très petit changement dans les dernières décimales des chiffres utilisés pour démarrer une simulation qui a provoqué ses résultats divergents. Ce que ni lui ni les autres n’ont compris, et qui est mis en évidence dans notre nouveau travail, est qu’une condition initiale (rationnelle) finie décrit un comportement qui peut être statistiquement hautement non représentatif » déclare Coveney.
Les chercheurs reconnaissent que la carte de Bernoulli est un système chaotique simple qui ne représente pas nécessairement des modèles dynamiques plus complexes, mais ils avertissent que la nature insidieuse de leur papillon à virgule flottante signifie qu’aucun scientifique ne devrait négliger ces risques.

