Après 32 ans de recherches, des scientifiques ont résolu l’énigme du neuvième nombre de Dedekind (à 42 chiffres), un problème mathématique complexe, grâce à l’utilisation du superordinateur Noctua. Cette découverte, qui a nécessité des techniques de calcul avancées, éclaire un aspect jusque-là inexploré des fonctions booléennes monotones. Elle démontre le potentiel des superordinateurs dans la résolution de problèmes mathématiques complexes et ouvre la voie à de nouvelles recherches dans ce domaine.
Certains mystères mathématiques qui régissent notre réalité, comme le nombre d’or, continuent d’émerveiller les chercheurs par leur complexité. Parmi ces derniers, certaines entités mathématiques ont suscité l’intérêt depuis leur découverte par Richard Dedekind à la fin du XIXe siècle. Certains problèmes complexes liés aux nombres concernent les « fonctions booléennes monotones », qui ont longtemps gardé leurs secrets — huit d’entre eux n’ont été résolus que récemment. Cependant, le problème du « neuvième nombre de Dedekind » est resté insaisissable pendant plus de trois décennies, posant un défi majeur à la communauté mathématique.
Récemment, une équipe de chercheurs de l’Université de Paderborn et de la KU Leuven a réussi à percer ce mystère notamment par le biais de l’utilisation innovante d’un superordinateur, le Noctua. Cet accomplissement, qui a nécessité des années de recherches et de calculs intensifs, marque une avancée significative dans le domaine des mathématiques et ouvre de nouvelles perspectives pour la résolution de problèmes complexes. Pour l’instant, il n’y a pas de rapport d’étude, mais cette dernière devrait être présentée en septembre lors de l’atelier international sur les fonctions booléennes et leurs applications (BFA), qui se tiendra en Norvège.
Les nombres de Dedekind, un concept complexe
Les nombres de Dedekind sont des entités mathématiques spéciales, des entiers qui jouent un rôle central dans l’étude des fonctions booléennes monotones. Il faut savoir que les fonctions booléennes sont une forme de logique mathématique qui opère sur des valeurs binaires, c’est-à-dire des valeurs qui peuvent prendre deux états distincts. Ces états peuvent être représentés de différentes manières : par vrai et faux, ou par 0 et 1. Dans le contexte des nombres de Dedekind, ces fonctions booléennes sont utilisées pour déterminer une sortie à partir d’un ensemble d’entrées binaires.
Les fonctions booléennes monotones sont une sous-catégorie de ces dernières. Elles ont une caractéristique particulière : elles sont conçues de telle manière que si l’on remplace un 0 par un 1 dans une entrée, cela ne provoque le changement de la sortie que de 0 à 1, et non l’inverse. En d’autres termes, ces fonctions sont « monotones » dans le sens où elles ne « reviennent » pas en arrière : une fois qu’une valeur a été changée de 0 à 1, elle ne peut pas être changée en sens inverse.
Lennart Van Hirtum, auteur principal de l’étude, explique dans un communiqué : « Fondamentalement, vous pouvez considérer une fonction booléenne monotone en deux, trois ou n dimensions comme un jeu avec un cube à n dimensions. Vous équilibrez le cube sur un coin, puis colorez chacun des coins restants en blanc ou en rouge. Il n’y a qu’une seule règle : il ne faut jamais placer un coin blanc au-dessus d’un coin rouge. Cela crée une sorte d’intersection verticale rouge-blanc. Le but du jeu est de compter le nombre de possibilités différentes. Leur nombre est ce qui est défini comme le nombre Dedekind. Même si cela n’en a pas l’air, les nombres deviennent rapidement gigantesques dans le processus : le 8e nombre Dedekind a déjà 23 chiffres ».
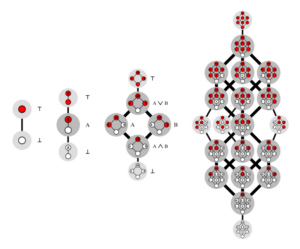
Ces fonctions jouent un rôle crucial dans de nombreux domaines des mathématiques et de l’informatique, notamment dans l’étude des structures de données, des algorithmes et de la théorie des graphes.
La résolution d’une énigme mathématique
La découverte du neuvième nombre de Dedekind, ou D(9), a été rendue possible grâce à l’utilisation de techniques de calcul avancées et de la puissance du superordinateur Noctua. Pour résoudre ce problème, les chercheurs ont utilisé une technique connue sous le nom de formule du coefficient P.
Cette formule offre une méthode pour calculer les nombres de Dedekind non pas en comptant, mais en effectuant une très grande somme. Cela a permis de décoder D(8) en seulement huit minutes sur un ordinateur portable normal. Cependant, ce qui prend huit minutes pour D(8) devient des centaines de milliers d’années pour D(9), même en utilisant un grand superordinateur.
Afin d’en venir à bout, les chercheurs ont dû recourir à des unités arithmétiques hautement spécialisées et parallèles appelées FPGA (Field Programmable Gate Arrays). Van Hirtum a développé un premier prototype de matériel conçu pour accélérer certains types de calculs informatiques. Puis, les chercheurs se sont tournés vers le superordinateur Noctua 2 du « Paderborn Center for Parallel Computing (PC2) » de l’Université de Paderborn, qui possède l’un des systèmes FPGA les plus puissants au monde.
Une découverte majeure
Après plusieurs années de développement, le programme a tourné sur le superordinateur pendant environ cinq mois. Et le 8 mars 2023, les scientifiques ont découvert le neuvième nombre de Dedekind : 286386577668298411128469151667598498812366. Cette découverte met en lumière la puissance impressionnante des superordinateurs et des techniques de calcul avancées.
Ces machines peuvent effectuer des milliards de calculs par seconde, avec des données massives, ce qui les rend indispensables pour résoudre des problèmes mathématiques complexes comme celui du neuvième nombre de Dedekind. Les techniques de calcul avancées, quant à elles, permettent de structurer et d’optimiser ces calculs pour tirer le meilleur parti de la puissance de ces superordinateurs.
Mais au-delà de la démonstration de la puissance des superordinateurs et des techniques de calcul avancées, cette découverte ouvre également la voie à de nouvelles recherches et découvertes dans le domaine des mathématiques. La résolution du neuvième nombre de Dedekind pourrait conduire à une meilleure compréhension des fonctions booléennes monotones et de leur application dans divers domaines, de l’informatique à la logique.

