Lorsque deux trous noirs se trouvent suffisamment proches l’un de l’autre pour que leur gravité mutuelle les attire, leurs orbites peuvent se stabiliser et donner naissance à un système binaire de trous noirs. Et lorsque ce phénomène concerne deux trous noirs supermassifs, les mécanismes impliqués sont encore plus impressionnants. Pour étudier le comportement de l’espace-temps et de la lumière dans un tel système, la NASA a publié une simulation montrant les extraordinaires effets physiques optiques générés par la gravité.
Une nouvelle modélisation de la NASA montre comment l’attraction extrême de la gravité plie et déforme la lumière dans les anneaux incandescents de gaz chaud encerclant les trous noirs dans un système binaire simulé. L’animation montre deux trous noirs : le plus gros de la paire, qui fait environ 200 millions de fois la masse de notre Soleil, est entouré d’un anneau rouge de gaz chaud appelé disque d’accrétion. En orbite autour de ce géant se trouve un deuxième trou noir pesant environ la moitié de cette masse, dont le disque est représenté en bleu.
De puissantes forces gravitationnelles tirent et déforment le tissu de l’espace-temps alors qu’un trou noir tourne autour de l’autre, pliant la lumière émise par les disques d’accrétion de chaque trou noir. Et plus vous vous rapprochez de l’un de ces géants déformés dans la simulation, plus l’autre apparaît tordu. « Zoomer sur chaque trou noir révèle de multiples images de plus en plus déformées de son partenaire », explique Jeremy Schnittman, astrophysicien au Goddard Space Flight Center (GSFC) de la NASA.
L’attraction gravitationnelle au centre d’un trou noir est si extrême que même la lumière ne peut pas s’échapper. En son cœur se trouve une région de densité infinie connue sous le nom de singularité, délimitée par l’horizon des événements. Juste à l’extérieur de l’horizon des événements, la gravité plie les photons en une courbe connue sous le nom de sphère de photons. Les anneaux de gaz et de poussière surchauffés du disque d’accrétion tournent autour de cette sphère, tourbillonnant à des vitesses incroyables et émettant des radiations électromagnétiques, telles que des rayons X, des ondes radio, des micro-ondes et des rayons gamma.
Visualiser les distorsions optiques dues à l’extrême gravité
La visualisation commence par une vue aérienne du plus petit trou noir en orbite autour du plus grand. Au début, ni l’un ni l’autre ne semble beaucoup affecté par la proximité de l’autre, mais cela change radicalement une fois que le point de vue se déplace vers le plan orbital. Désormais, lorsqu’un trou noir passe devant l’autre, la lumière de l’objet d’arrière-plan se tord et s’enroule pour suivre la distorsion gravitationnelle.
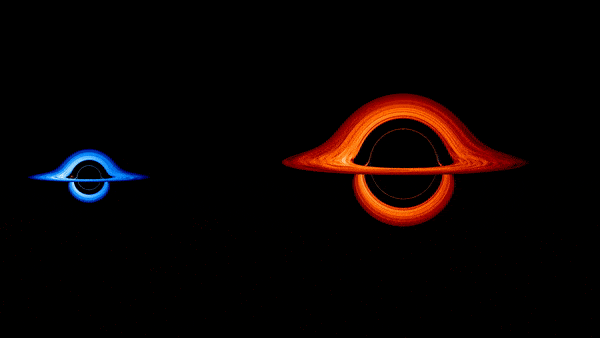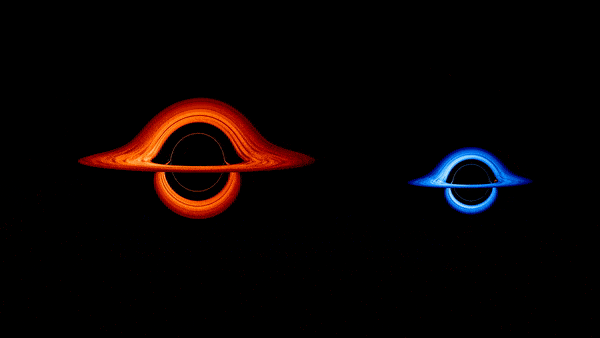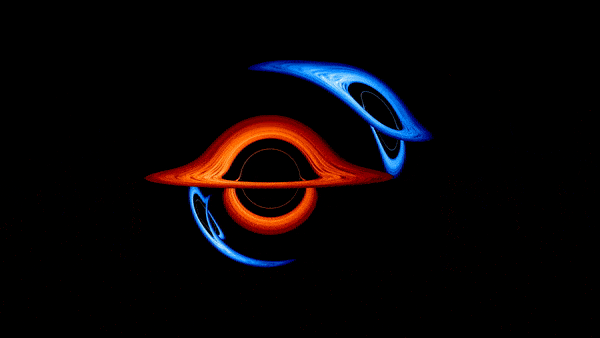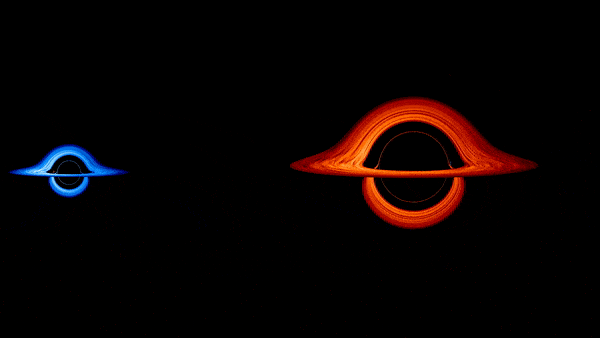
Les couleurs visuellement brillantes dans la simulation sont des choix artistiques, car les disques d’accrétion des trous noirs supermassifs émettraient de la lumière dans la gamme ultraviolette du spectre. Pour créer la simulation, Schnittman a calculé comment la lumière produite dans les disques d’accrétion se courberait autour du tissu déformé de l’espace-temps pendant la danse des trous noirs. Il a calculé les mouvements image par image en une journée environ, en utilisant le cluster de superinformatique Discover du Centre de simulation climatique de la NASA.
Les systèmes binaires de trous noirs supermassifs
On pense que la plupart des grandes galaxies abritent un trou noir supermassif en leur centre. Les systèmes binaires de trous noirs supermassifs proviennent de collisions de galaxies, bien que dans la plupart des cas, les trous noirs se mettent à spiraler l’un autour de l’autre de sorte que seule une fraction des galaxies fusionnées retiennent deux trous noirs en orbite.
Dans de tels systèmes où les deux trous noirs sont supermassifs, cette distorsion de la lumière peut persister très longtemps. « Ce sont les types de systèmes binaires de trous noirs dans lesquels nous pensons que les deux membres pourraient maintenir des disques d’accrétion pendant des millions d’années », conclut Schnittman.
Simulation des déformations optiques dans le cas d’un système binaire de trous noirs :
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]
Une galaxie est une grande structure cosmique composée d'un
assemblage d'étoiles, de gaz et de poussières. Il en existe
plusieurs types, classés selon leur masse et leur morphologie,
formées à différentes... [...]