L’effervescence médiatique autour du dernier article écrit par le physicien Stephen Hawking en collaboration avec Thomas Hertog, et présenté comme « l’ultime théorie d’Hawking », n’est toujours pas retombée. Cependant, même si cet article demeure intéressant et comporte de remarquables développements, son contenu scientifique ne peut être qualifié de « révolutionnaire », tant il est loin de toutes les interprétations que les journaux en ont fait.
Suite au décès du physicien Stephen Hawking, l’annonce d’une nouvelle théorie publiée peu avant sa mort émerge au sein de la communauté médiatique. Cette nouvelle, dont l’emphase croît à chaque reprise par les journaux, provoque un fulgurant effet boule de neige et finit par présenter le papier co-rédigé par Hawking comme « révolutionnaire » et « bouleversant ». Dès lors, des articles sensationnels fleurissent un peu partout sur Internet, à commencer par les « grands journaux ».
The Independant affirme ainsi que le papier comporte « une théorie expliquant comment nous pouvons détecter des univers parallèles ainsi qu’une prédiction sur la fin de l’univers […]. Hawking a également théorisé dans ses travaux finaux que des scientifiques pourraient détecter l’existence d’univers alternatifs en utilisant des sondes embarquées sur des vaisseaux spatiaux ». Quant au Sunday Times, celui-ci explique que l’étude « démontre comment nous pourrions détecter d’autres univers ». The Times parle même du « plus grand héritage de Stephen Hawking », celui-ci ayant trouvé « les mathématiques requises pour détecter l’existence du multivers ».
En résumé, Stephen Hawking aurait résolu l’énigme du Big Bang en offrant une méthode expérimentale déterminante pour prouver l’existence du multivers, tout en livrant une étonnante prédiction sur le destin final de notre univers. Des travaux qui lui garantiraient assurément le prix Nobel selon les médias. Mais de quel article s’agit-il ? L’article en question, intitulé A Smooth Exit from Eternal Inflation ? (lien en fin d’article), rédigé par Stephen Hawking et le physicien belge Thomas Hertog, a été publié pour la première fois sur arXiv le 24 juillet 2017, puis complété le 4 mars 2018 (soit 10 jours avant le décès de Hawking).
Toutefois, très loin de ces diverses affirmations journalistiques grandiloquentes, un examen attentif du papier en question révèle que si ce dernier est effectivement intéressant et propose de remarquables développements, force est de constater qu’il est tout sauf révolutionnaire. Cette situation est malheureusement commune et symptomatique de l’absence d’analyse critique de la part des médias, ce qui finit par totalement biaiser le véritable travail des scientifiques. De quoi parle alors exactement ce papier ?
L’univers sans bord : le modèle de Hartle-Hawking
L’article de Hawking et de Hertog est basé sur une théorie initialement proposée par le physicien britannique et le physicien américain James Hartle afin de résoudre le problème de la singularité initiale, et d’offrir une description quantique de l’espace-temps au voisinage du Big Bang. Les équations de la relativité générale d’Albert Einstein montrent qu’en remontant le temps jusqu’au moment du Big Bang, l’univers est contenu dans une singularité gravitationnelle primordiale. Cette singularité indique une « pathologie » de la théorie d’Einstein, c’est-à-dire son incapacité mathématique à décrire le commencement de l’univers. En effet, à cette période, les effets quantiques de la gravité sont dominants, et nécessitent donc une théorie de la gravité quantique pour être décrits.
En 1983, Hartle et Hawking proposent un modèle cosmologique visant à contourner le problème de la singularité initiale. Pour ce faire, ils introduisent la notion de « temps imaginaire » dans leurs calculs. En mécanique quantique, le temps imaginaire, au sens mathématique du terme, n’est plus décrit par les nombres réels usuels mais par les nombres complexes ; le temps réel peut ainsi être représenté horizontalement – le temps s’écoule de gauche à droite, du passé vers le futur, tandis que le temps imaginaire peut être représenté verticalement – aucune direction temporelle n’est privilégiée. L’association de trois dimensions spatiales et d’une dimension temporelle imaginaire donne un espace-temps euclidien.
Dans ce modèle, les physiciens traitent l’univers comme une fonction d’onde. En mécanique quantique, la fonction d’onde donne l’état quantique d’une particule. Elle est calculée à l’aide de l’équation de Schrödinger, dont les solutions peuvent être formulées en termes d’intégrale. En 1942, le physicien Richard Feynman introduit la notion d’intégrale de chemin, qui offre une reformulation de la mécanique quantique ; techniquement, elle permet une formulation lagrangienne de la mécanique quantique plutôt qu’hamiltonienne. Les intégrales de chemin ont permis de grandement simplifier les calculs en théorie quantique des champs, concernant la description des interactions fondamentales du Modèle Standard.
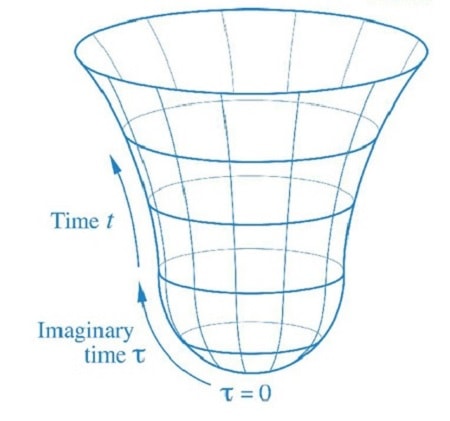
Hartle et Hawking associent donc une fonction d’onde à l’univers, dont les paramètres sont calculés via l’intégrale de chemin de Feynman. En introduisant un temps imaginaire, la notion d’espace-temps disparaît car le temps imaginaire, de par sa nature, est décrit comme une dimension spatiale. L’espace-temps usuel à 4 dimensions devient ainsi simplement un espace à 4 dimensions. Cela donne lieu à un espace-temps quantique possédant une topologie sphérique dont l’espace et le temps imaginaire seraient finis mais sans limites.
Dans sa conférence intitulée « The beginning of Time », Stephen Hawking prend l’exemple de la Terre pour décrire la géométrie de l’espace-temps imaginaire proche du Big Bang : « l’espace et le temps imaginaires sont comme la surface de la Terre mais avec deux dimensions supplémentaires. La surface de la Terre est finie mais elle ne possède aucune limite ou bord ». C’est pourquoi les deux physiciens ont appelé leur modèle l’ « univers sans bord ». Dans ce modèle, l’univers débute bien à partir d’un point, mais il ne s’agit pas d’une singularité. Hawking le compare au pôle Nord de la Terre : « il s’agit d’un point d’espace et de temps tout à fait ordinaire, comme le pôle Nord est un point tout à fait ordinaire à la surface de la Terre ».
Ce modèle prédit que durant l’inflation cosmique, les fluctuations quantiques ont été si violentes qu’elles ont laissé leurs empreintes dans les ondes gravitationnelles primordiales. Ainsi que l’explique Hawking, « l’inflation aurait laissé l’univers presque totalement lisse, mais avec quelques irrégularités ». En 1992, la mission Cosmic Background Explorer satellite (COBE) a identifié des fluctuations (anisotropies) dans le fonds diffus cosmologique pouvant correspondre aux prédictions du modèle de Hartle-Hawking.
Inflation, inflation éternelle, multivers et modèle de Hawking-Hartle
En 1979, le physicien Alan Guth introduit la notion d’inflation pour résoudre le problème de l’horizon. Ainsi, aussitôt après le Big Bang, l’univers aurait connu une dilatation extrêmement brève et violente qui expliquerait l’homogénéité et l’isotropie de l’univers. Cependant, la solution de Guth est problématique car elle amène les faux vides (état du vide instable) à se transformer en bulles de vrais vides, et donc ne contient aucun mécanisme mettant fin à l’inflation. La solution, appelée « nouvelle inflation », est apportée en 1982 par Andrei Linde et Paul Steinhardt, qui introduisent l’inflaton (champ à pression négative), c’est-à-dire un mécanisme permettant d’évoluer lentement du faux vide vers le vrai vide sans création de bulles, tout en mettant fin à l’inflation.
En 1983, Paul Steinhardt montre que cette nouvelle inflation ne s’arrête pas nécessairement partout dans l’univers. Au lieu de cela, elle peut s’arrêter dans certaines zones, formant ainsi des bulles de matière et de rayonnement, pour ensuite continuer dans d’autres zones. Dans ce scénario, l’univers serait ainsi toujours en inflation. Ce modèle a donc été baptisé « inflation éternelle ». La même année, Steinhardt, Alexander Vilenkin et d’autres physiciens montrent que les bulles générées par l’inflation éternelle forment des univers déconnectés les uns des autres, et la notion de multivers apparaît.
Durant les années 2000, Hawking, Hartle et Hertog travaillent activement sur la cohérence de l’inflation éternelle appliquée au modèle d’univers sans bord. En 2002, ils décrivent l’origine quantique de l’inflation cosmique dans le cadre de leur modèle en montrant qu’à ses débuts, l’univers était un univers de de Sitter instable (univers homogène et isotrope, vide de matière et rempli d’une constante cosmologique positive, c’est la géométrie que l’on retrouve dans le modèle inflationnaire actuel). En 2006, ils étudient le paysage de la théorie des cordes et son multivers toujours dans le cadre de l’univers sans bord, et proposent un moyen de tester la théorie. En 2012, grâce au principe holographique, ils établissent une connexion entre un univers de de Sitter et un univers anti-de Sitter (univers vide de matière et rempli d’une constante cosmologique négative). De nombreux autres articles ont été écrits par les trois physiciens à propos de ces sujets.
Article de Hawking et Hertog : l’holographie pour décrire le multivers de l’inflation éternelle
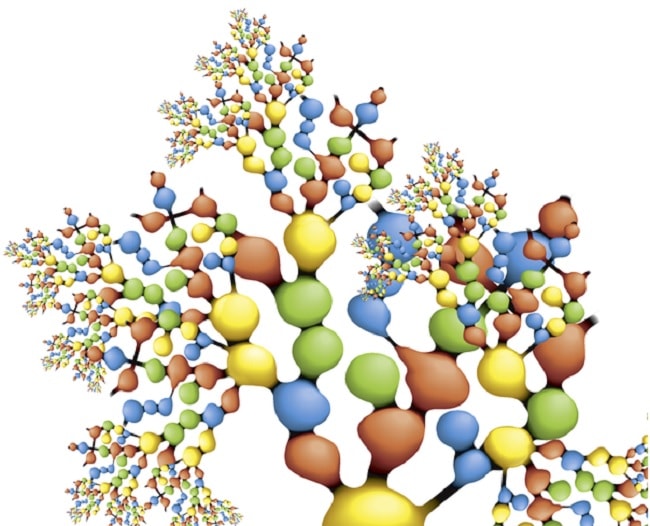
Dans leur papier, Hawking et Hertog se basent sur le modèle d’univers sans bord pour décrire les paramètres des univers contenus dans le multivers de l’inflation éternelle si cette théorie s’avère correcte. Avant d’aller plus loin, il est nécessaire de rappeler que lorsque Steinhardt introduit le scénario de l’inflation éternelle, celui-ci démontre que la topologie du multivers, plus précisément la géométrie des zones de l’univers dans lesquelles l’inflation s’est arrêtée, est naturellement fractale et chaotique.
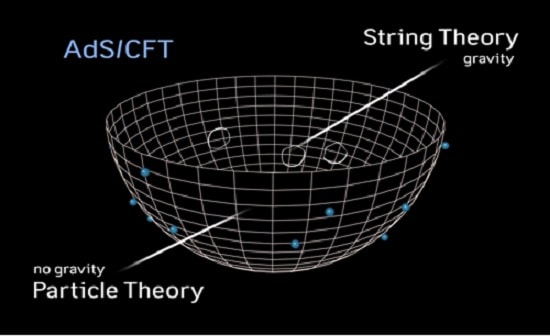
En 1998, le physicien théoricien argentin Juan Maldacena introduit un outil mathématique établissant une correspondance entre deux types de théories : d’un côté, les théories des champs conformes (CFT) qui sont des théories quantiques des champs et d’un autre, les théories de la gravité quantique basées sur un espace anti-de Sitter (AdS). Cette correspondance est appelée « correspondance AdS/CFT » ou encore « dualité de Maldacena ».
Celle-ci permet de passer d’une théorie à l’autre pour simplifier certains calculs. Par exemple, lorsque les champs sont fortement couplés en CFT, les calculs sont éminemment complexes à effectuer ; en revanche, ces mêmes champs se retrouvent faiblement couplés en théorie gravitationnelle quantique (AdS), les calculs sont donc plus faciles à réaliser dans ce cadre. Ainsi, le fait de passer d’une théorie à l’autre, comme si l’on « projetait » les calculs d’un espace à un autre, fait de la correspondance AdS/CFT un puissant outil du principe holographique.


Avant les travaux de Maldacena, effectuer des calculs de géométrique dans un espace-temps quantique était relativement compliqué, au point de devoir se satisfaire de solutions approchées tant les équations étaient difficilement solubles. C’est pourquoi le modèle d’univers sans bord développé initialement par Hawking et Hartle s’accommodait mal du scénario de l’inflation éternelle, aboutissant à des incohérences physico-mathématiques.
Dans leur article, Hawking et Hertog ont utilisé la correspondance AdS/CFT dans le but de modifier les calculs initiaux du modèle d’univers sans bord, afin de les rendre cohérents avec l’inflation éternelle. Techniquement, les physiciens ont recalculé la fonction d’onde de l’univers en montrant que les théories à gravité quantique dans un espace anti-de Sitter (AdS) contiennent un champ scalaire à pression négative qui, dans une théorie impliquant un espace de de Sitter (dS/CFT), correspond au champ inflaton de l’inflation éternelle.
En d’autres mots, les calculs étaient trop complexes à effectuer dans l’espace de de Sitter (dS), c’est-à-dire la géométrie de l’univers lors de l’inflation dans notre modèle cosmologique actuel. Alors les auteurs ont effectué ces calculs dans un espace anti-de Sitter (AdS), dans lequel il existe un champ scalaire à pression négative qui peut être assimilé au champ inflaton (champ à pression négative) de l’univers de de Sitter. Hawking et Hartle ont ainsi bien reconnecté le modèle d’univers sans bord avec l’inflation éternelle.
Ces calculs amènent ces derniers à redéfinir les paramètres du multivers né de l’inflation éternelle. Tout d’abord, le multivers ne serait plus infini mais posséderait une topologie bien délimitée, finie dans l’espace. En outre, loin d’être aussi chaotique que l’univers fractal déterminé par Steinhardt, il serait bien plus lisse et régulier. Enfin, les calculs réduisent considérablement l’ensemble des univers possibles. L’article est donc intéressant dans le sens où il offre un moyen mathématique de déterminer certains éléments du multivers.
En revanche, l’article ne décrit absolument aucun moyen expérimental pour tester cette hypothèse. Rien, dans ce papier, n’indique comment détecter, prouver ou observer l’existence du multivers. Les auteurs n’expliquent à aucun moment comment nous pourrions tester les hypothèses qu’ils formulent et, en cela, cet article reste purement théorique et spéculatif. Il ne comporte également aucune mention du fond diffus cosmologique ou de la polarisation des ondes gravitationnelles primordiales. Pour couronner le tout, le destin de l’univers n’y est jamais abordé. En bref, si l’article intègre des éléments dignes d’intérêt, il ne mérite en aucun cas la portée révolutionnaire qui lui est attribuée. Nous sommes donc encore loin du prix Nobel.