Face à la complexité de la classification des formes géométriques élémentaires, des chercheurs ont envisagé une approche novatrice : créer un « tableau périodique des formes », à l’image de celui des éléments chimiques. Dans le cadre de récents travaux de recherche, l’intelligence artificielle, avec ses capacités d’apprentissage rapide, a été utilisée avec succès pour faciliter cette tâche.
La géométrie, pilier fondamental des mathématiques, s’est toujours efforcée de décrypter et de classifier les formes qui nous entourent. Cette discipline, comme de nombreuses autres, connaît actuellement un gain de productivité grâce à l’intervention de l’intelligence artificielle.
Des chercheurs de l’Imperial College de Londres et de l’Université de Nottingham aspirent à créer un « tableau périodique des formes », similaire à celui des éléments chimiques. Ce tableau permettrait de classer et de mieux comprendre certaines des formes les plus élémentaires, dont les « formes atomiques », qui ne peuvent être décomposées davantage. Leurs travaux sont publiés dans la revue Nature Communications.
Les variétés de Fano : des formes indivisibles
Les variétés de Fano représentent une catégorie particulière de formes géométriques qui se distinguent par leur simplicité fondamentale. À l’instar des atomes, qui constituent les unités de base de la matière et ne peuvent être subdivisés en particules plus élémentaires, ces variétés sont les blocs de construction élémentaires de la géométrie. Elles possèdent une structure intrinsèque qui ne permet pas de les décomposer davantage.
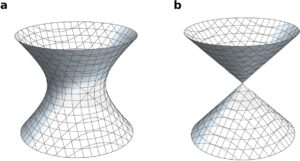
Cependant, malgré leur simplicité apparente, les variétés de Fano présentent une complexité sous-jacente qui pose un véritable casse-tête aux mathématiciens. Leur classification nécessite une compréhension approfondie de leurs propriétés et de leurs relations mutuelles. Tout comme les chimistes ont dû étudier en détail les propriétés des atomes pour établir le tableau périodique des éléments, les mathématiciens sont confrontés à la tâche ardue de catégoriser ces formes primordiales.
Ce défi est d’autant plus grand que, contrairement aux atomes, qui peuvent être observés et étudiés à l’aide d’instruments tels que les microscopes électroniques, les variétés de Fano sont des entités purement mathématiques. Leur étude nécessite donc des outils et des méthodes spécifiques à la géométrie, ainsi qu’une approche conceptuelle pour saisir leur essence.
La période quantique : une empreinte unique pour les variétés de Fano
Chaque variété de Fano possède une caractéristique distincte appelée « période quantique », expliquent les auteurs dans un communiqué. Cette séquence numérique joue un rôle similaire à celui d’un code-barres ou d’une empreinte digitale pour un objet ou une personne : elle permet d’identifier de manière unique la variété en question. Bien que les chercheurs aient postulé que cette période quantique pourrait déterminer la dimension de la variété de Fano, le mécanisme exact derrière cette relation est resté jusqu’ici énigmatique. En l’absence d’une théorie solide à ce sujet, il était difficile de valider cette hypothèse sur l’ensemble des variétés de Fano identifiées.
C’est ici que l’apprentissage automatique, une branche de l’intelligence artificielle, entre en jeu. Ces algorithmes sont spécialement conçus pour détecter des tendances et des motifs dans de vastes ensembles de données. En fournissant à un modèle d’apprentissage automatique un échantillon de données sur les variétés de Fano et leurs périodes quantiques, l’équipe de recherche a pu entraîner ce modèle à reconnaître et à prédire les relations entre ces variétés. Les résultats ont été impressionnants : le modèle formé a permis de prédire la dimension des variétés de Fano en se basant uniquement sur leurs périodes quantiques, avec une fiabilité remarquable de 99%.
Interaction entre l’IA et les mathématiques : « une symbiose bénéfique »
L’approche adoptée par l’équipe de recherche illustre parfaitement la complémentarité entre les méthodes traditionnelles et les outils modernes. Bien que le modèle d’intelligence artificielle ait fourni des indications précieuses sur la relation entre la période quantique et la dimension des variétés de Fano, il ne suffisait pas à lui seul pour établir une preuve formelle. Les chercheurs ont donc combiné les prédictions de l’IA avec des techniques mathématiques éprouvées pour valider cette relation, utilisant l’IA comme une boussole pour orienter leurs investigations.
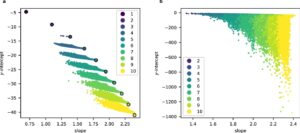
Au-delà de cette application spécifique, l’équipe a souligné l’importance des données mathématiques dans le développement et l’affinement des modèles d’apprentissage automatique. Contrairement aux données issues du monde réel, souvent entachées d’irrégularités et de bruits, les données mathématiques offrent une clarté et une précision inégalées. Elles sont dépourvues de ces perturbations aléatoires qui peuvent brouiller les modèles.
Le professeur Tom Coate, du département de mathématiques de l’Imperial College de Londres, conclut : « L’intelligence artificielle pourrait réellement révolutionner les mathématiques, car nous avons montré que l’apprentissage automatique est un outil puissant pour repérer des modèles dans des domaines complexes comme l’algèbre et la géométrie ».
En les exposant à des données « pures », les chercheurs peuvent améliorer la capacité des modèles à reconnaître et à interpréter des motifs complexes. Comme le tableau périodique des éléments a révolutionné la chimie, un tableau périodique des formes pourrait transformer notre compréhension des formes géométriques. Il pourrait également ouvrir la voie à de nouvelles découvertes en physique, en biologie et dans d’autres branches des sciences.

