Les trous de ver sont des objets cosmiques hypothétiques qui constitueraient un raccourci entre un point A et un point B de l’espace, l’espace-temps entre l’entrée (un trou noir) et la sortie (un trou blanc) étant comme « replié » sur lui-même. Selon certaines études antérieures, ce « passage » entre les deux orifices spatio-temporels serait trop instable pour permettre à un objet quelconque de s’y aventurer, tandis que d’autres indiquent qu’un trou de ver se romprait dès sa formation. Mais une nouvelle étude vient contredire ces prédictions et propose un modèle de trou de ver stable et traversable.
En début d’année, nous vous présentions déjà une étude proposant un modèle de trou de ver « traversable », suggérant des hypothèses et des équations élégantes, bien que légèrement incomplètes, basées sur la théorie d’Einstein-Dirac-Maxwell. Aujourd’hui, Pascal Koiran, un astrophysicien de l’École Normale Supérieure de Lyon, et ses collègues, annoncent eux aussi avoir élaboré une théorie montrant que les trous de ver sont bien des structures astrophysiques hypothétiques stables, mais en se basant cette fois-ci sur la métrique d’Eddington-Finkelstein.
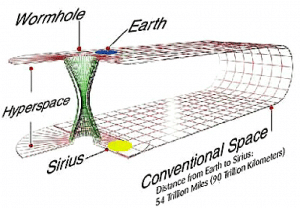
Si ces structures étaient stables, cela signifierait qu’un objet — capable d’en subir toutes les contraintes mécaniques — pourrait voyager à des vitesses extrêmes (du point de vue d’un voyageur qui n’emprunterait pas le raccourci) entre la sortie et l’entrée d’un trou de ver, comme cela est notamment représenté dans certaines oeuvres de science-fiction (Interstellar, pour citer la plus marquante de ces dernières années). Ces connexions spatio-temporelles sont connues sous le nom de « ponts d’Einstein-Rosen ».
Métrique d’Eddington-Finkelstein : rendre traversables les trous de ver
Dans la littérature scientifique, il est communément admis que les forces extrêmes à l’intérieur d’un trou de ver forcent ce dernier à s’étirer et à se rompre comme un élastique dès sa formation. Mais Albert Einstein et Natan Rosen, pionniers de cette théorie, ont bâti leur modèle de trou de ver sur la métrique habituelle de Schwarzschild, et la plupart des modèles de trous de ver utilisent cette même métrique.
Dans leur nouvelle étude, Koiran et ses collègues utilisent donc une autre approche, basée sur la métrique d’Eddington-Finkelstein, qu’ils décrivent dans un article disponible sur le serveur de préimpression arXiv, et qui devrait être publié prochainement dans la revue Journal of Modern Physics D.
Les coordonnées utilisées dans leur modèle sont obtenues, par transformations (de la variable temporelle), à partir de celles de Schwarzschild. Et c’est cette transformation qui amène l’ingrédient principal aboutissant à un tout autre résultat concernant la stabilité de l’objet.
Passer outre l’horizon des événements d’un trou noir
« Il est bien connu qu’une masse test tombant dans un trou noir n’atteint pas l’horizon des événements pour toute valeur finie de la variable temporelle t de Schwarzschild. En revanche, nous montrons que l’horizon des événements est atteint pour une valeur finie de la variable temporelle t′ d’Eddington-Finkelstein », écrivent les chercheurs dans leur document.
Une fois avoir montré que l’horizon des événements d’un trou noir — la limite à partir de laquelle tout objet ou lumière ne peut s’échapper de son attraction gravitationnelle — était atteignable dans leur modèle de trou de ver d’Eddington-Finkelstein, ils ont calculé comment une particule massive traversant un pont d’Einstein-Rosen réagirait. Ils montrent alors que, non seulement la particule atteindrait l’entrée du trou noir, mais elle continuerait sa trajectoire à travers le « tunnel » spatio-temporel, jusqu’à éventuellement atteindre la sortie. Elle serait ainsi éjectée par le trou blanc — qui à l’inverse du trou noir, ne fait qu’expulser de la matière.
« Un tel comportement n’a pas de sens avec la variable temporelle de Schwarzschild, puisqu’il reviendrait à poursuivre la trajectoire de la particule ‘au-delà de la fin des temps’ », concluent les chercheurs dans leur document. Ils suggèrent ainsi que leur modèle serait plus « logique » que les précédents (communément admis) pour expliquer le comportement d’un trou de ver.
Bien entendu, cela n’apporte pas la preuve irréfutable que les trous de ver sont stables et traversables. En effet, il y a bien d’autres facteurs à considérer au-delà de la théorie de la relativité générale, qui pourraient démontrer qu’un tel objet est en réalité « impossible » ou instable en dehors des modèles mathématiques. Des modèles qui, d’ailleurs, empruntent eux-mêmes un certain nombre de raccourcis — imposés par les limites de notre compréhension de l’espace-temps et des forces en jeu.
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]