Le carré, le triangle, le losange, le cercle et le trapèze sont parmi les formes géométriques les plus familières. Pourtant, malgré cette apparente exhaustivité, la nature continue de nous étonner. Récemment, des mathématiciens ont mis au jour une nouvelle classe de figures géométriques, capables de remplir entièrement un espace en deux ou trois dimensions. Nommées « cellules molles », ces formes se retrouvent notamment dans les cellules musculaires ou dans les coquilles de mollusques, telles que celle du nautile, avec ses structures tridimensionnelles incurvées.
Depuis longtemps, les mathématiciens se passionnent pour le pavage, cette science de l’agencement optimal des formes pour recouvrir une surface sans laisser de vide ni de chevauchement. Traditionnellement, les solutions géométriques privilégient les figures aux angles définis, telles que les triangles, les hexagones et les polyèdres, pour couvrir intégralement un plan en deux dimensions. Néanmoins, la nature semble suivre des règles bien différentes.
Alain Goriely, professeur de modélisation mathématique à l’Université d’Oxford et co-auteur de la nouvelle étude, déclare dans un communiqué : « La nature a non seulement horreur du vide, mais elle semble aussi détester les angles aigus ». Des exemples de cette aversion se retrouvent dans la coquille du nautile, la coupe transversale d’un oignon avec ses couches concentriques, ou encore les cellules musculaires, organisées en mosaïques circulaires. Les mathématiciens se sont donc heurtés à un défi de taille en tentant de déchiffrer comment la nature parvient à une telle complexité géométrique avec ces « formes douces ».
Inspirée par les pavages de Penrose découverts dans les années 1980, une équipe conduite par Gábor Domokos de l’Université de technologie et d’économie de Budapest, en collaboration avec des mathématiciens de l’Université d’Oxford, a trouvé une solution. Dans une étude publiée dans PNAS Nexus, les chercheurs ont réexaminé les pavages polygonaux périodiques. Ils ont ainsi identifié une nouvelle classe de formes géométriques : les cellules molles. Selon l’équipe, ces formes « minimisent le nombre d’angles aigus et sont capables de couvrir un espace sans chevauchement ».

Deux expériences avec des résultats divergents
Dans le cadre de leurs recherches, Domokos et ses collègues ont mené des expériences à partir d’un nouveau modèle algorithmique. Ils ont découvert que, dans un espace bidimensionnel, les cellules molles ne présentent que deux coins. Ce type de motif se retrouve couramment dans certaines conceptions architecturales, les cellules musculaires et les couches d’oignons, entre autres. Toutefois, ces cellules molles révèlent une complexité accrue dans un espace tridimensionnel. « Les cellules molles contribuent à expliquer pourquoi, lorsque l’on regarde une coupe transversale d’une coquille à chambres, on voit des coins, mais pas la géométrie 3D des chambres », explique Domokos.
En étudiant les chambres nautiloïdes, les mathématiciens ont observé des angles aigus dans les coupes transversales. Cependant, dans la structure tridimensionnelle interne, ils ont constaté une figure géométrique plus fluide, dépourvue de bords définis, et présentant des caractéristiques de pavage différentes. Domokos souligne que l’étude approfondie des coquilles de nautile a été surprenante : leurs coupes transversales ressemblent à des cellules molles en 2D, mais avec deux coins.
Krisztina Regős, co-auteure de l’étude, a déclaré : « Malgré la présence de deux coins dans le plan, il m’a semblé qu’il n’y avait pas de coins en trois dimensions ». En effet, lorsque les chercheurs ont observé des images CT détaillées, ils ont constaté que les chambres du Nautilus sont des cellules molles qui remplissent la coquille sans aucun coin.
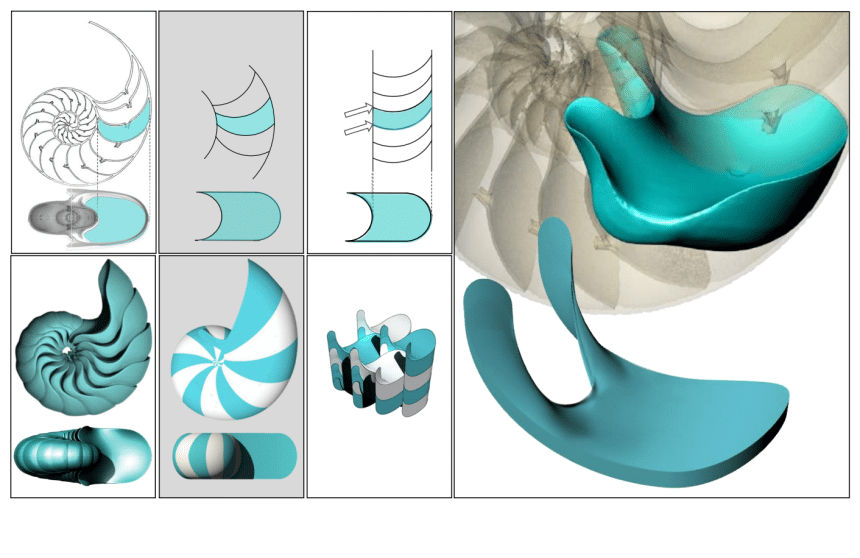
« L’univers des pavages polygonaux et polyédriques est si fascinant et riche que les mathématiciens n’ont pas eu besoin d’élargir leur terrain de jeu », a ajouté Domokos. « L’absence d’angles vifs et leur géométrie douce et très courbée font des cellules molles des modèles candidats idéaux pour les structures biologiques qui ont évolué sous contrainte totale ou partielle pour remplir l’espace », concluent les chercheurs.

