Des mathématiciens ont mis en évidence une nouvelle catégorie de formes géométriques présentes en abondance dans la nature. Ces formes, contrairement aux figures conventionnelles, correspondent mieux à la structure complexe des éléments naturels.
Les formes géométriques peuvent être définies par des équations précises et sont marquées par des contours nets et des points acérés. Ces caractéristiques les rendent facilement analysables du point de vue géométrique. Cependant, les formes géométriques connues jusqu’ici ne correspondent pas toujours à celles trouvées dans la nature. En effet, les éléments naturels tendent à présenter des contours plus complexes, des surfaces courbes et des structures irrégulières qui ne sont pas facilement décrites par des équations simples.
Cela a récemment motivé des mathématiciens de l’Université de technologie de Budapest à explorer de nouvelles formes géométriques et à développer des théories mathématiques qui pourraient mieux cerner la diversité et la complexité des formes naturelles.
Ils ont ainsi identifié une nouvelle classe de formes, qu’ils ont nommées « soft cells » (cellules souples). Ces formes se caractérisent par leurs bords incurvés et l’absence de coins durs, ce qui les distingue nettement des formes géométriques conventionnelles. À travers cette découverte, le travail des chercheurs hongrois devrait contribuer à améliorer notre compréhension de l’implication des mathématiques dans la modélisation des phénomènes naturels. Les détails sont disponibles sur le serveur de prépublication arXiv.
Une application dans le pavage de l’espace dans les éléments naturels
Ces nouvelles figures — les soft cells — sont décrites comme des sortes de tuiles possédant des bords incurvés. Et malgré cette forme non conventionnelle, elles peuvent s’agencer pour former des structures cohérentes tant en deux et en trois dimensions. Selon les chercheurs, elles peuvent effectivement être déformées « en douceur » afin de former des tuiles souples.
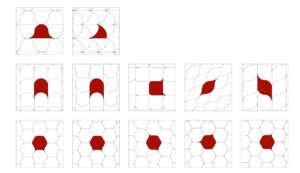
Un aspect très intéressant de ces nouvelles figures est leur application dans le « pavage de l’espace » chez les éléments naturels, qui a jusqu’ici constitué l’un des problèmes élémentaires de la géométrie, selon les chercheurs de l’étude. À titre informatif, le pavage fait référence à la couverture d’une surface ou d’un volume avec des formes répétitives, sans chevauchement ni espace vide. Dans les éléments naturels, les pavages ne suivent pas toujours ces règles géométriques strictes. Pour cause : l’irrégularité de leurs surfaces et l’absence relative d’angles vifs dans leurs structures.
Des formes répandues dans la nature
Par ailleurs, les chercheurs ont constaté que ces formes nouvellement décrites sont largement répandues dans la nature. Ils citent notamment de nombreux objets naturels, tels que les cellules biologiques, les coquillages et peut-être même certains types de tissus organiques, qui présentent des caractéristiques géométriques s’éloignant des formes rigides étudiées en mathématiques.
Concernant l’implication de cette découverte, la correspondance de ces formes pour le pavage de différentes structures 2D et 3D pourrait potentiellement se traduire par des applications dans divers domaines, tels que la biologie (où elles pourraient offrir des modèles adaptés à la structure des tissus vivants) ou l’ingénierie, où ces formes géométriques pourraient inspirer la conception de structures plus efficaces et durables.


