Au niveau fondamental, l’Univers est composé de particules interagissant les unes avec les autres au sein de l’espace-temps. Toutefois, ces paramètres ne sont pas suffisants, à eux seuls, pour décrire correctement l’Univers. En effet, il est nécessaire de rajouter à ce tableau les constantes décrivant l’intensité des différentes interactions et les propriétés physiques des particules. Nous avons ainsi besoin de 26 constantes fondamentales pour décrire l’Univers et, même en considérant ce nombre important, la description est incomplète.
Un électron, par exemple, pourrait interagir avec un autre électron. Il possède une charge fondamentale (ou élémentaire) qui lui est associée (notée e), et une masse fondamentale (notée me). Les électrons s’attirent gravitationnellement les uns les autres, proportionnellement à l’intensité de la force gravitationnelle G et se repoussent électromagnétiquement, inversement proportionnellement à la force de la permittivité de l’espace ε0.
Il existe d’autres constantes qui jouent un rôle majeur dans le comportement de ces particules, comme la vitesse de la lumière, c, et la constante fondamentale associée aux transitions quantiques : la constante de Planck, ħ. Mais les physiciens n’aiment pas utiliser ces constantes lorsqu’il s’agit de décrire l’univers, car ces dernières ont des dimensions et des unités arbitraires.
Une unité comme le mètre, le kilogramme ou la seconde n’a aucune importance inhérente. Peu importe les unités utilisées, les lois de la physique se comporteraient exactement de la même manière. En réalité, il est possible de décrire tous les phénomènes de l’Univers sans définir une unité fondamentale de « masse », de « temps » ou de « distance ». Nous pourrions décrire les lois de la nature, dans leur totalité, en utilisant uniquement des constantes sans dimension.
Une constante sans dimension est une constante purement numérique. Il s’agit simplement d’un nombre sans unité. Si en utilisant cette méthode pour décrire l’Univers l’on arrive à retrouver les lois fondamentales et les conditions initiales correctes, il serait donc possible de retrouver toutes les propriétés mesurables de l’Univers. Cela inclut des éléments tels que les masses de particules, les forces d’interaction, les limites de vitesse de l’information et même les propriétés fondamentales de l’espace-temps.
Sur le même sujet : Les constantes fondamentales définiront bientôt les unités du Système International
1) La constante de structure fine
Notée α, c’est une constante de couplage décrivant l’intensité de l’interaction électromagnétique. Elle est obtenue par la charge élémentaire e élevée au carré, divisée par le produit de la constante de Planck ħ et de la vitesse de la lumière dans le vide c. Bien que dimensionnées, la combinaison de ces trois constantes donne une constante sans dimensions. Au niveau d’énergie actuel de l’Univers, celle-ci vaut α ≈ 1/137.036. Cette valeur varie avec l’énergie des particules mises en jeu.
2) La constante de couplage de l’interaction forte
Notée αs, c’est une constante de couplage décrivant l’intensité de l’interaction forte. Bien que le mécanisme de cette dernière soit très différent de celui de l’électromagnétisme ou de la gravité, la force de cette interaction peut quand même n’être paramétrée que par une seule constante de couplage. Sa valeur varie également selon l’énergie mise en jeu.
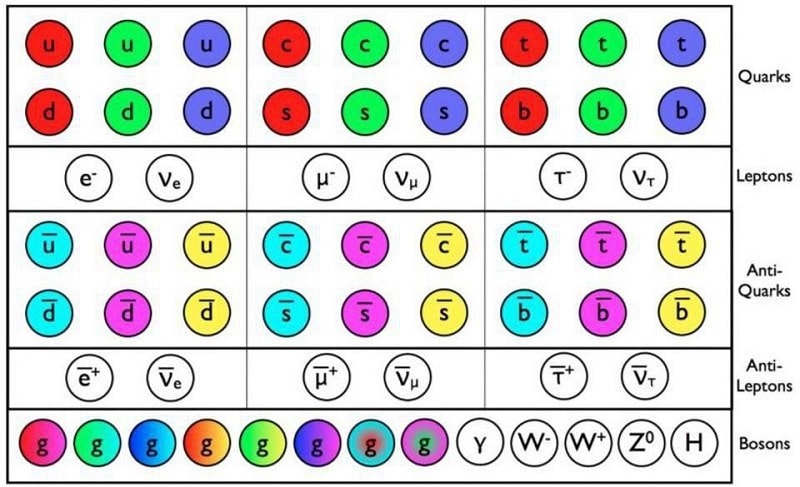
3 à 17) La masse des six quarks, des six leptons et des trois bosons massifs
Le Modèle Standard compte six saveurs de quarks et six types de leptons, tous massifs et classés dans la catégorie des fermions. Dans la catégorie des bosons, seuls les bosons W/Z (bosons de l’interaction nucléaire faible) et le boson de Higgs sont massifs. Cependant, le nombre de paramètres requis pour décrire la masse de ces particules est trop haut, et les physiciens espéraient découvrir une théorie de la masse plus simple.
Les chercheurs ont pensé qu’une telle théorie sous-jacente pouvait exister, considérant l’existence de certaines relations entre les particules. Par exemple, la collision d’un positron à 45 GeV avec un électron à 45 GeV donne la quantité d’énergie exacte pour produire un boson Z ; la collision d’un positron à 45 GeV avec un électron au repos, donne la quantité d’énergie exacte pour produire une paire de muon/anti-muon.
Toutefois, en approfondissant les calculs, il s’avère que ces relations sont approximatives. L’énergie requise pour créer un boson Z est plus proche de 46 GeV, tandis que celle nécessaire pour créer une paire muon/anti-muon est plus proche de 44 GeV. En l’absence d’une théorie plus fondamentale, la description de la masse des particules du modèle standard requiert donc 15 constantes.
18 à 21) Les paramètres du mélange des quarks
Sur les six saveurs de quarks, quatre possèdent des nombres quantiques identiques et peuvent donc se mélanger. Ces probabilités de mélange (transformation d’un quark en un autre sous l’effet de l’interaction faible) sont données par la matrice de Cabibbo-Kobayashi-Maskawa (matrice CKM). Des phénomènes comme l’interaction faible, la désintégration radioactivite ou la violation CP, dépendent directement de ces quatre paramètres de mélange des quarks.
22 à 25) Les paramètres d’oscillation des neutrinos
Il existe trois saveurs de neutrino : le neutrino électronique, le neutrino muonique et le neutrino tauique. Initialement, les physiciens pensaient que les neutrinos possédaient une masse nulle. Toutefois, l’anomalie des neutrinos solaires — détection d’une quantité de neutrinos solaires trop faible par rapport aux prédictions — a nécessité de repenser le modèle des neutrinos en considérant des neutrinos de masse très faible, mais pas nulle, et un mécanisme d’oscillation.
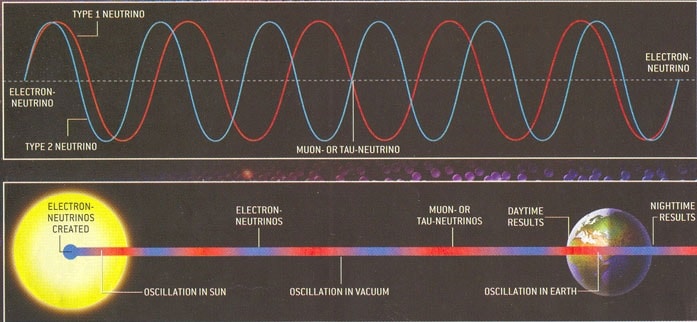
L’oscillation des neutrinos est le processus au cours duquel un neutrino se transforme en un autre type de neutrino au cours de sa propagation. De la même manière que pour le mélange des quarks, les probabilités d’oscillation des neutrinos est donnée par une matrice unitaire, la matrice de Pontecorvo-Maki-Nakagawa-Sakata (matrice PMNS). Mais contrairement aux quarks, seuls trois paramètres ont été mesurés pour les neutrinos, le dernier (la phase de violation CP) demeure toujours inconnu.
26) La constante cosmologique
L’Univers est en expansion accélérée, et cette accélération est actuellement expliquée par l’hypothèse de l’énergie sombre, nécessitant donc l’introduction d’un paramètre supplémentaire, la constante cosmologique, pour décrire cette accélération. Cependant, l’énergie sombre pourrait s’avérer bien plus complexe qu’une simple constante, ce qui nécessiterait l’introduction de paramètres supplémentaires, portant le total au-delà de 26.
En donnant aux physiciens les lois physiques fondamentales, les conditions initiales de l’Univers et ces 26 constantes, ils pourront simuler n’importe quel aspect de l’Univers. Toutefois, ces constantes ne permettent pas à elles seules d’expliquer tous les phénomènes de l’Univers. Actuellement, il existe quatre grands problèmes qui pourraient nécessiter l’ajout de constantes additionnelles : l’asymétrie matière/antimatière, l’inflation cosmique, la matière noire et la violation CP forte.
L’électron est une particule élémentaire qui, avec les protons et
les neutrons, constitue les atomes. C’est donc l’un des composants
principaux de la matière baryonique. À ce titre, il revêt... [...]
