Les trous de ver font partie des solutions existantes aux équations d’Einstein de la relativité générale. Ils consistent en un tunnel traversant l’espace-temps, permettant de relier deux points distants en seulement quelques secondes. Les premières solutions de type trou de ver trouvées par les physiciens impliquent des systèmes instables requérant une énergie négative, élément jugé généralement impossible par la physique classique. Récemment, deux physiciens ont montré que, dans des conditions particulières impliquant une physique au-delà du Modèle Standard, la mécanique quantique autorise l’existence de trous de vers traversables et stables pour l’Homme. Si les conditions nécessaires ne sont pour le moment pas celles de l’Univers que nous observons, ces résultats montrent la puissance théorique des interactions entre relativité générale et mécanique quantique.
Dans une nouvelle étude réalisée par deux physiciens théoriciens, l’existence d’une physique au-delà du modèle standard pourrait signifier qu’il existe des trous de ver qui sont non seulement assez grands pour être traversables, mais entièrement sûrs pour les voyageurs humains qui cherchent à se rendre d’un point A à un point B. L’étude a été menée par Juan Maldacena et Alexey Milekhin. Le duo a beaucoup écrit sur le sujet des trous de ver dans le passé et comment ils pourraient être un moyen de voyager en toute sécurité dans l’espace.
La théorie concernant les trous de ver a émergé au début du 20e siècle, en réponse à la théorie de la relativité générale d’Einstein. Le premier à postuler leur existence fut Karl Schwarzschild, un physicien et astronome allemand dont les solutions à l’équation du champ d’Einstein (la métrique de Schwarzschild) ont abouti à la première base théorique de l’existence des trous noirs.
Une conséquence de la métrique de Schwarzschild était ce qu’il appelait les « trous noirs éternels », qui étaient essentiellement des connexions entre différents points de l’espace-temps. Cependant, ces trous de ver de Schwarzschild (encore appelés ponts d’Einstein–Rosen) n’étaient pas stables car ils s’effondraient trop rapidement pour que quoi que ce soit passe d’un bout à l’autre.
Une énergie négative permise par la mécanique quantique
Comme Maldacena et Milekhin l’expliquent, les trous de ver traversables nécessitent des circonstances spéciales pour exister. Cela inclut l’existence d’énergie négative, ce qui n’est pas permis en physique classique — mais est possible dans le domaine de la physique quantique. Un bon exemple de cela, affirment-ils, est l’effet Casimir, où les champs quantiques produisent de l’énergie négative tout en se propageant le long d’un cercle fermé.
Ils écrivent dans leur article : « nous nous sommes rendus compte que cet effet pouvait devenir considérable pour les trous noirs à forte charge magnétique. La nouvelle idée était d’utiliser les propriétés spéciales des fermions sans masse chargés (particules comme l’électron, mais de masse nulle). Pour un trou noir chargé magnétiquement, ceux-ci voyagent le long des lignes de champ magnétique (d’une manière similaire à la façon dont les particules chargées du vent solaire créent les aurores à proximité des régions polaires de la Terre) ».
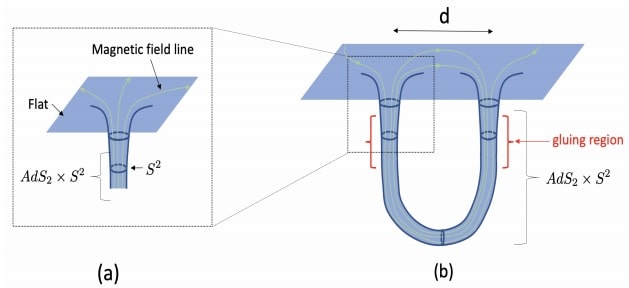
Le fait que ces particules puissent se déplacer en cercle en entrant dans un endroit et en émergeant là où elles ont commencé dans l’espace plat ambiant, implique que « l’énergie du vide » est modifiée et peut être négative. La présence de cette énergie négative peut soutenir l’existence d’un trou de ver stable, un pont entre des points de l’espace-temps qui ne s’effondrera pas avant que quelque chose n’ait une chance de le traverser.
De tels trous de ver sont possibles sur la base de la matière qui fait partie du modèle standard de la physique des particules. Le seul problème est que ces trous de ver devraient être de taille microscopique et n’existeraient que sur de très petites distances. Pour les déplacements humains, les trous de ver devraient être grands, ce qui nécessite l’utilisation de la physique au-delà du modèle standard.
Des trous de vers réalisables dans le modèle d’univers à 5 dimensions de Randal-Sundrum II
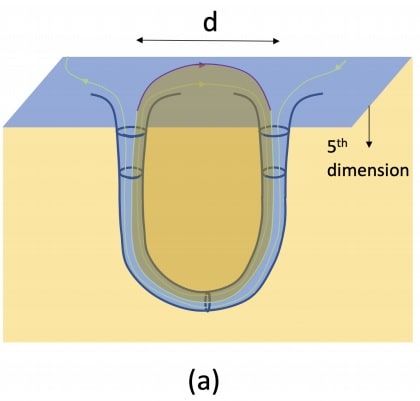
Pour Maldacena et Milekhin, c’est là que le modèle Randall-Sundrum II (alias la théorie de la géométrie déformée en 5 dimensions) entre en jeu. Nommé d’après les physiciens théoriciens Lisa Randall et Raman Sundrum, ce modèle décrit l’Univers en termes de cinq dimensions et a été initialement proposé pour résoudre un problème de hiérarchie en physique des particules.
Sur le même sujet : Des physiciens montrent qu’il est théoriquement possible de stabiliser un trou de ver pour le traverser
« Le modèle Randall-Sundrom II était basé sur la prise de conscience que cet espace-temps à cinq dimensions pourrait également décrire la physique à des énergies plus faibles que celles que nous explorons habituellement, mais qu’il aurait échappé à la détection car il ne se couple avec notre matière que par gravité. En fait, sa physique est similaire à l’ajout de nombreux champs sans masse fortement interactifs à la physique connue. Et pour cette raison, il peut donner naissance à l’énergie négative requise ».
Selon les travaux de Maldacena et Milekhin, leurs trous de ver ne prendraient presque pas de temps à traverser du point de vue du voyageur. Du point de vue d’un observateur extérieur, le temps de trajet serait beaucoup plus long, ce qui est cohérent avec la relativité générale. Pour les astronautes qui traversent le trou de ver, il ne faudrait qu’une seconde de leur temps pour parcourir 10’000 années-lumière. Un observateur qui ne passe pas par le vortex et reste à l’extérieur, les voit prendre plus de 10’000 ans. Et tout cela sans utilisation de carburant, car la gravité accélère et décélère le vaisseau spatial.
Un mécanisme théorique intéressant, mais peu réaliste
Bien que cela puisse sembler encourageant pour ceux qui pensent que les trous de ver pourraient être un jour un moyen de voyager dans l’espace, les travaux de Maldacena et Milekhin présentent également des inconvénients importants. Pour commencer, ils soulignent que les trous de ver traversables devraient être conçus en utilisant une masse négative, car aucun mécanisme plausible n’existe pour leur formation naturelle.
Bien que cela soit possible (au moins en théorie), les configurations d’espace-temps nécessaires devraient être présentes à l’avance. Même ainsi, la masse et la taille impliquées sont si grandes que la tâche dépasse toute technologie pratique que nous pouvons prévoir. Deuxièmement, ces trous de ver ne seraient sûrs que si l’espace est froid et plat, ce qui n’est pas le cas au-delà du modèle Randall Sundrum II.
En plus de tout cela, tout objet qui pénètre dans le trou de ver serait accéléré et même la présence d’un rayonnement de fond cosmique constituerait un danger important. Cependant, Maldacena et Milekhin soulignent que leur étude a été menée dans le but de montrer que des trous de ver traversables peuvent exister en raison de « l’interaction subtile entre la relativité générale et la physique quantique ».
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]
L’électron est une particule élémentaire qui, avec les protons et
les neutrons, constitue les atomes. C’est donc l’un des composants
principaux de la matière baryonique. À ce titre, il revêt... [...]
L'année-lumière est une unité de longueur utilisée pour exprimer
des distances astronomiques. Elle est définie par l'Union
Astronomique Internationale (UAI) comme la distance parcourue par
la lumière dans le vide pendant une année julienne (365.25 jours).
Elle vaut environ... [...]