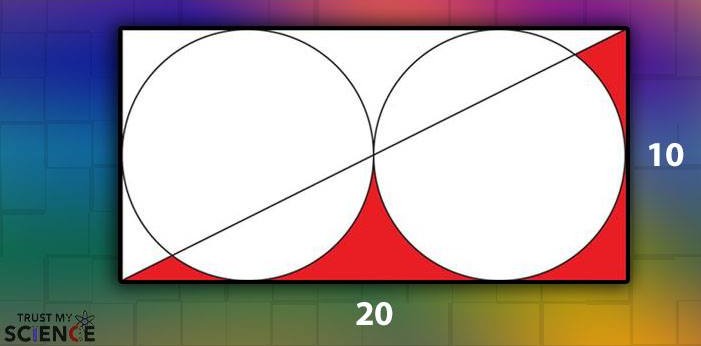
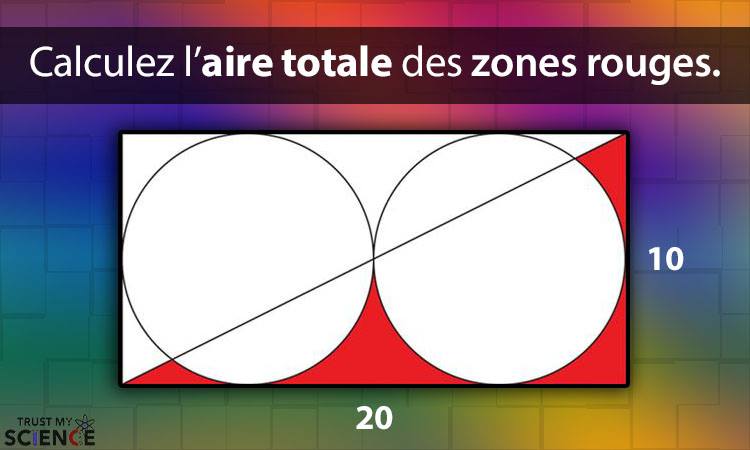
Arriverez-vous à résoudre ce petit casse-tête ? Le but étant de trouver l’aire totale des zones rouges.
Voici les données :
Vous avez un rectangle qui mesure 20 unités de long et 10 unités de haut. Le rectangle est traversé par une diagonale. À l’intérieur du rectangle, il existe deux cercles de même taille qui sont tangents l’un à l’autre ainsi qu’au rectangle. La zone en dessous de la ligne diagonale à l’intérieur du rectangle est remplie en rouge, mais l’intérieur des cercles qui sont en dessous de la ligne diagonale ne le sont pas.
Quelle est la superficie des zones rouges ?
Nous vous laissons réfléchir un moment. Puis, ci-dessous, découvrez la vidéo montrant comment trouver la réponse. Une version plus complexe du casse-tête est également présentée.
VIDÉO : Arriver à la réponse !
La réponse :
Elle est toute simple. L’aire des zones rouges est obtenue par 100 (la moitié de l’aire du rectangle) – 25 π (l’aire d’un des cercles), ce qui équivaut à 21,460. Si vous avez de la peine, regardez la vidéo ci-dessus afin de comprendre comment arriver à ce résultat.