Dans le cadre de la gravité newtonienne, toutes les masses exercent une force d’attraction les unes sur les autres, dépendant de la distance et de la masse de chacune. Dans le contexte de la relativité générale, toute masse est source de gravité par la déformation de la géométrie de l’espace-temps. Qu’en est-il alors des particules de masse nulle ? Sont-elles également affectées par la gravité ?
Lorsqu’Isaac Newton a proposé pour la première fois sa loi de la gravité universelle, c’est une véritable révolution qui a vu le jour. La même loi qui expliquait la chute des objets sur Terre expliquait également les mouvements et l’attraction des corps dans tout l’Univers. Les objets tombent sur Terre à cause de la gravité ; les planètes ont une forme de sphéroïde à cause de la gravité ; les lunes orbitent les planètes, et les planètes orbitent le Soleil à cause de la gravité.
La gravité de Newton : une loi universelle pour les corps massifs
La loi de la gravitation de Newton est simple mais profonde : les objets massifs s’attirent les uns les autres en fonction de leur masse, leur distance, et de la constante gravitationnelle. Multiplier la constante gravitationnelle par deux masses quelconques, divisées par la distance au carré entre ces dernières, suffisait à exprimer universellement la gravité.
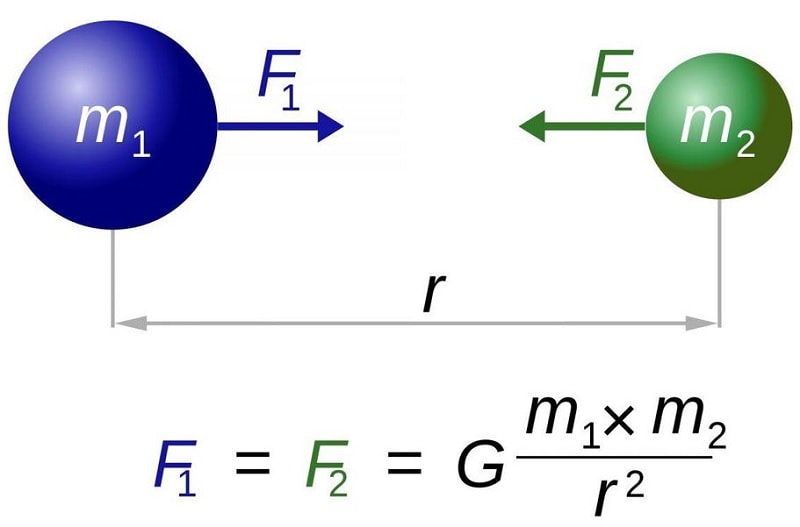
Cette loi permettait d’expliquer tous les types d’orbites : cercles, ellipses, paraboles et hyperboles. Elle permettait d’expliquer l’énergie potentielle gravitationnelle, et la transformation de celle-ci en énergie cinétique. Elle expliquait également la vitesse de libération et comment échapper à l’attraction terrestre. Pendant près de 200 ans, la gravitation newtonienne a permis de résoudre tous les problèmes impliquant la gravité.
Voilà toute l’essence de la gravité universelle : elle s’exerce instantanément en tout point de l’Univers entre tous les objets massifs. Toutefois, avec le perfectionnement des instruments d’observation, de nombreux problèmes d’ordre cosmologique ont commencé à entacher la loi de Newton. Notamment l’observation de la courbure de la lumière aux abords des objets massifs, qui s’avérait incompatible avec une loi ne tenant uniquement compte que de la masse pour décrire la gravité.
La relativité générale : énergie et courbure de l’espace-temps
En outre, de nombreux indices remettaient en cause un autre grand postulat de la gravité newtonienne : la rigidité de l’espace-temps. Plus précisément, pour Newton, espace et temps sont deux entités différentes, séparées, rigides et immuables. Il a fallu attendre les travaux d’Albert Einstein sur la relativité générale, en 1915, pour comprendre que pour être correcte et rendre compte fidèlement des observations effectuées, une théorie de la gravité doit être vraie pour n’importe quel observateur, dans n’importe quel référentiel.

Une telle assertion a donc nécessité des postulats radicalement différents de ceux de Newton. Dans la relativité générale, espace et temps ne forment plus qu’une seule entité, l’espace-temps, dynamique et relative, dont chaque observateur à une vision aussi valide et correcte que les autres. Cet espace-temps est déformable sous l’effet de contraintes qui lui sont appliquées. La source de ces déformations n’est plus la masse, mais l’énergie, dont la masse n’est qu’une forme. Et cette déformation se propage à la vitesse de la lumière dans le vide, non instantanément.
Sur le même sujet : L’espace-temps, courbé par la masse ou par l’énergie ?
Ainsi, toute source d’énergie peut déformer la géométrie de l’espace-temps et est à l’origine d’un champ gravitationnel. C’est donc le cas des particules de masse nulle comme le photon qui, même sans masse, dispose tout de même d’une énergie non-nulle (qui ne se calcule pas avec la formule E=mc² puisque le photon n’est au repos dans aucun référentiel, mais avec la formule E=hv, où « h » est la constante de Planck et « v » la fréquence du photon), et est donc également la source d’un champ gravitationnel.
Trajectoires dans l’espace-temps courbé : des géodésiques imposées aux photons
L’équation d’Einstein montre clairement la relation entre la géométrie de l’espace-temps et la distribution d’énergie-matière. Matière et énergie courbent l’espace-temps, et l’espace-temps courbé indique à la matière et l’énergie comment se déplacer. Ainsi, contrairement à la gravité newtonienne où les planètes orbitent le Soleil uniquement à cause de la force d’attraction gravitationnelle, dans la relativité générale, les planètes se déplacent dans la courbure de l’espace-temps produite par le Soleil.
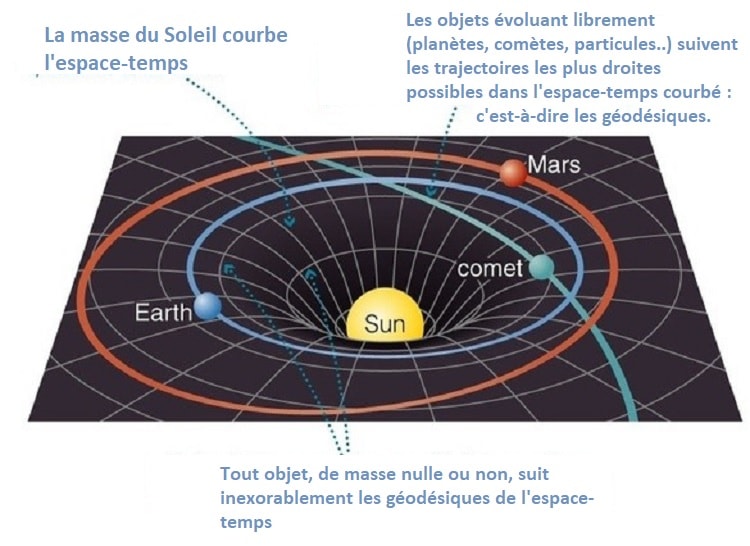
Ces trajectoires courbes dans l’espace-temps s’appellent des géodésiques. En d’autres mots, la généralisation d’une ligne droite dans un espace courbé est une géodésique. Les planètes suivent donc les géodésiques autour du Soleil. De la même manière, les photons se déplacent toujours en ligne droite ; donc lorsqu’une source d’énergie ou de matière courbe l’espace-temps sur leur trajectoire, ils sont obligés de suivre les géodésiques ainsi formées. C’est de cette manière que les particules de masses nulles sont affectées par la gravité.

