Publiée en 1915, la théorie de la relativité générale a révolutionné notre compréhension de l’univers en offrant une vision novatrice de la gravitation. Le pilier central de la théorie d’Einstein est l’équation du champ gravitationnel dont les différentes solutions, que les physiciens continuent de mettre en évidence aujourd’hui, décrivent la grande variété de structures de l’espace-temps issues de la théorie.
Le 25 novembre 1915, Albert Einstein soumet pour la première fois ses travaux sur la relativité générale à l’Académie royale des sciences de Prusse. L’article en question contient le fondement mathématique de la théorie : l’équation d’Einstein, encore appelée équation du champ gravitationnel. Cette équation aux dérivées partielles décrit l’intime relation entre la masse-énergie et l’espace-temps. Plus précisément, elle décrit la manière dont la matière et l’énergie modifient la géométrie de l’espace-temps.
Dès lors, cette équation rompt avec la définition traditionnelle de la gravitation selon Newton. En effet, avec cette équation, la gravité n’est plus une force qui s’exerce entre deux corps, mais elle se manifeste à travers la courbure de l’espace-temps. Et cette courbure s’interprète comme le champ gravitationnel de la source qui en est à l’origine. Les corps en mouvement empruntent des géodésiques, c’est-à-dire des trajectoires définies dans l’espace-temps dont la description passe par l’équation de la géodésique.
L’équation d’Einstein prend généralement la forme suivante :
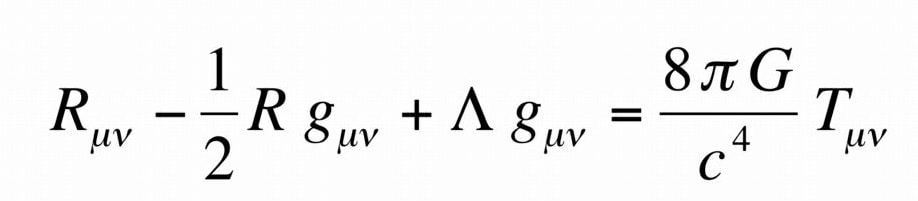
Chaque « côté » de l’égalité a une signification précise. À gauche, se trouvent les termes relatifs à la géométrie de l’espace-temps. Dans l’ordre d’apparition :
- Rμv est le tenseur de Ricci, c’est un tenseur d’ordre 2 décrivant la déformation de l’espace-temps
- gμv est le tenseur métrique, c’est un tenseur d’ordre 2 déterminant le produit scalaire de deux vecteurs dans l’espace, il permet de décrire la géométrie de l’espace-temps (longueurs et angles)
- R est la courbure scalaire, c’est un outil renseignant sur la courbure de l’espace-temps en assignant à chaque point de l’espace, un nombre réel caractérisant la courbure en ce point
- Λ est la constante cosmologique, c’est un paramètre correspondant à la densité d’énergie moyenne du vide (rajoutée par Einstein le 8 février 1917, pour obtenir un univers statique)
À droite, se trouvent les termes relatifs au contenu énergie-matière de l’espace-temps. Dans l’ordre d’apparition :
- G est la constante gravitationnelle
- π et c sont respectivement le nombre Pi et la vitesse de la lumière dans le vide
- Tμv est le tenseur énergie-impulsion, c’est un tenseur d’ordre 2 décrivant la répartition énergie-masse dans l’espace-temps
La forme de cette équation montre donc clairement une relation entre le contenu masse-énergie et la géométrie de l’espace-temps. Elle permet ainsi de décrire la courbure de l’espace-temps en fonction de la présence de masse-énergie. L’équation du champ gravitationnel possède certaines propriétés remarquables comme la conservation locale de l’énergie ou encore la possibilité de retomber sur l’équation de la gravité newtonienne lorsque le champ gravitationnel devient faible (approximation des champs faibles).
L’équation d’Einstein possède plusieurs solutions qui consistent à chercher les différentes valeurs du tenseur métrique gμv. Ces solutions, qui décrivent la géométrie de l’espace-temps en fonction de la distribution en masse-énergie, se nomment donc des « métriques ». Une métrique est un outil mathématique permettant de décrire la configuration de l’espace-temps. Ainsi, selon la valeur de gμv, la métrique obtenue décrira une structure particulière de l’espace-temps. Une solution à cette équation désigne donc une valeur spécifique de gμv.
La recherche de solutions exactes à l’équation du champ est un exercice extrêmement compliqué car certains termes (Rμv et R) sont directement liés à la métrique (gμv) et donnent donc lieu à 10 équations « secondaires » non-linéaires ; c’est-à-dire que la somme de deux solutions de ces équations ne constitue pas une solution à son tour (les solutions sont indépendantes). En cosmologie théorique, la recherche de solutions exactes à l’équation d’Einstein est un domaine actif de recherche pour l’élaboration de modèles physico-mathématiques cohérents.
Plusieurs métriques ont ainsi été mises en évidence depuis la publication de la relativité générale, parmi lesquelles :
- la métrique de Minkowski qui décrit un espace-temps vide de matière et d’énergie dénuée d’influence gravitationnelle ; elle implique donc un tenseur énergie-impulsion nul, soit Tμv = 0. C’est l’espace-temps de la relativité restreinte.
- la métrique de Schwarzschild qui décrit l’espace-temps autour d’une distribution sphérique de masse-énergie statique ; par exemple une étoile ou un trou noir
- la métrique de Kerr qui décrit l’espace-temps autour d’un trou noir en rotation non chargé (absence de champ magnétique)
- la métrique de Kerr-Newman qui décrit l’espace-temps autour d’un trou noir en rotation chargé (présence de champ magnétique)
- la métrique de Reissner-Nordström qui décrit l’espace-temps autour d’un trou noir statique chargé
- la métrique FLRW (Friedmann-Lemaître-Robertson-Walker) qui décrit un espace-temps homogène et isotrope en expansion (c’est la métrique utilisée dans le modèle cosmologique standard Λ-CDM)


 Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]
Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]