De quelle manière un photon perçoit-il l’Univers ?

Au début du 20ème siècle, Albert Einstein révolutionne notre vision de l’Univers en montrant que l’espace et le temps sont relatifs pour des observateurs situés dans des référentiels différents. Plus la vitesse d’un observateur, relativement à son environnement, est élevée et s’approche de celle de la lumière, plus des effets relativistes émergent. Mais qu’en est-il dans le cas d’un photon qui se déplace strictement à la vitesse de la lumière dans le vide ? Comment, dans ce cas, perçoit-il l’Univers ?

Plus de 100 ans après sa formalisation par Albert Einstein, la relativité restreinte demeure l’une des théories les plus complexes et abouties permettant de décrire l’Univers.

Les lois de la physique newtonienne restent valides pour des vitesses très inférieures à la vitesse de la lumière dans le vide. Mais dès que ces vitesses deviennent relativistes, les horloges sont désynchronisées, les distances sont altérées et même la couleur des objets change en fonction de leur vitesse relative à l’observateur.

Parallèlement à cela, la relativité affirme que les lois physiques sont identiques et invariantes pour tous les observateurs, indépendamment de leur mouvement. Qu’en est-il alors pour un photon se déplaçant exactement à la vitesse de la lumière dans le vide (notée « c ») ?

Pour répondre à cette question, il est intéressant de considérer trois situations différentes : un observateur au repos, un observateur se déplaçant à une vitesse relativiste, et un observateur se déplaçant à c (c’est-à-dire le photon).

1. Dans le cas d’un observateur au repos

Au repos par rapport à son environnement, le temps de l’horloge d’un observateur s’écoule tout à fait ordinairement. C’est également le cas pour les horloges alentours. Les couleurs des objets apparaissent normales, leurs tailles sont respectées et l’Univers paraît ce qu’il doit être peu importe la direction dans laquelle il est observé.

Il s’agit ici de la vision commune du monde qu’expérimente tout observateur au repos sur Terre, où les vitesses humaines sont très, très inférieures à c. Même à bord d’un avion de ligne, se déplaçant proche de la vitesse du son, un voyageur ne se déplace qu’à 0.0001% de c. Au repos par rapport à ce qui l’entoure, un observateur perçoit l’Univers de la même façon que tous les autres.

2. Dans le cas d’un observateur se déplaçant à une vitesse relativiste

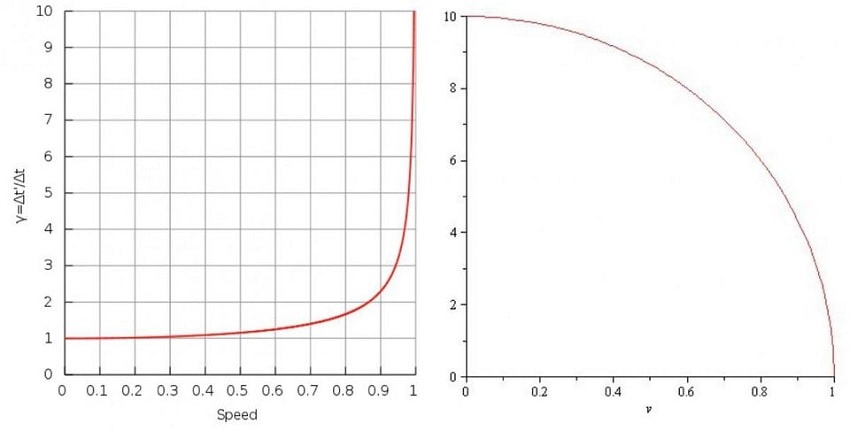
Voyageant à une vitesse relativiste dans une direction particulière, par rapport à son environnement stationnaire, la première différence notée par l’observateur est relative au temps. Bien que le temps de son horloge continue de s’écouler normalement (son temps propre reste inchangé), il n’en va pas de même pour les horloges alentours, qui paraissent fonctionner au ralenti.

Sur le même sujet : Comment les particules de masse nulle sont-elles affectées par la gravité ?

En outre, les longueurs et distances sont contractées dans la direction du mouvement. Cela est requis par la relativité pour que la vitesse de la lumière dans le vide demeure invariante pour tous les observateurs dans tous les référentiels : si le temps est ralenti (moins de temps) alors les distances doivent être contractées (moins de distance) afin que c reste constante.

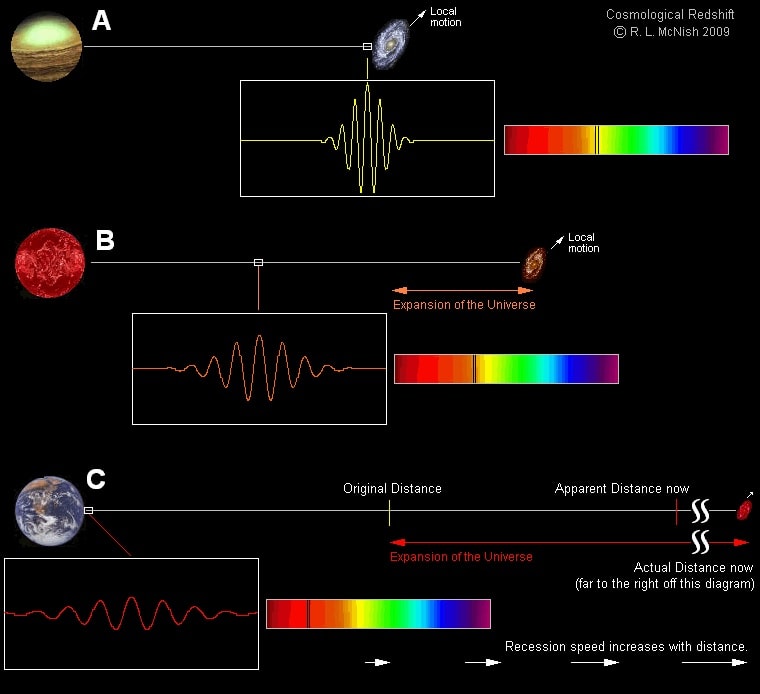
Enfin, en plus de la dilatation temporelle et de la contraction des longueurs, des phénomènes de décalage de longueur d’onde entrent en jeu— le décalage vers le bleu (blueshift) et vers le rouge (redshift). Dans la direction du mouvement, la longueur d’onde de la lumière est compressée, elle devient plus courte et tend vers le bleue. Dans la direction opposée, elle est étirée, elle devient donc plus longue et tend vers le rouge.

Plus la vitesse est élevée, plus ces effets sont accentués. Même les champs électriques produits par les particules chargées sont contractés dans la direction de leur mouvement. Le temps se dilate encore plus fortement ; les muons produits dans la haute atmosphère parviennent à parcourir les 100 km jusqu’à la surface terrestre alors que leur temps de vie n’est que de 2.2 microsecondes.

Et les phénomènes de redshift et blueshift deviennent si importants que les photons du fond diffus cosmologique peuvent produire spontanément de nouvelles particules, en entrant en collision avec des protons à des blueshifts suffisamment hauts. Cependant, même si tous ces effets sont aggravés par la vitesse, il existe une limite physique correspondant exactement à c.

3. Cas d’un observateur se déplaçant à la vitesse de la lumière dans le vide (photon)

En s’approchant de plus en plus près de c, les effets cités plus haut deviennent de plus en plus importants. Les pommes apparaîtraient jaunes, puis bleues puis dans les UV en se déplaçant vers elles ; tandis que les bananes apparaîtraient jaunes, puis oranges, puis rouges, puis dans les infrarouges en se déplaçant dans la direction opposée.

Mais pour une vitesse strictement égale à c, l’espace et le temps ne se comporteraient plus comme à l’ordinaire. Le temps propre de l’observateur devient nul ; il est impossible de définir une horloge. Les distances et longueurs dans la direction du mouvement sont contractées à zéro. Et les redshifts et blueshifts deviennent infinis.

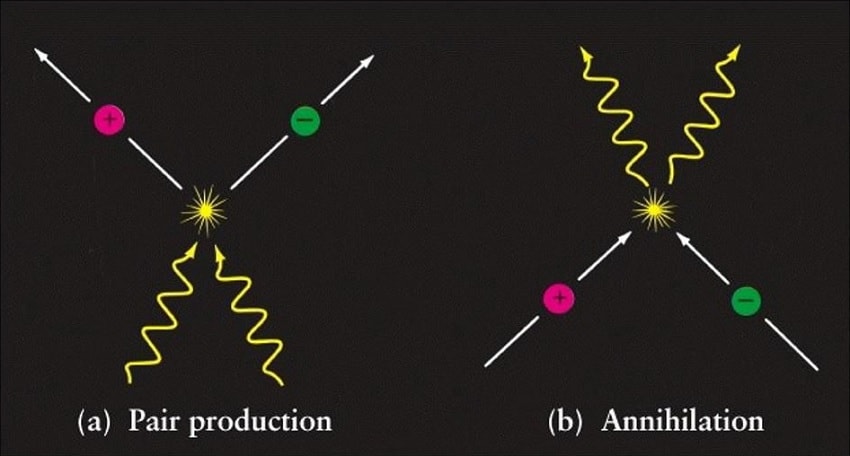
Dès lors, il serait intuitif de penser que, puisque les distances sont contractées jusqu’à zéro dans le sens du mouvement, l’Univers apparaît en deux dimensions, sans temps, comme un plan : avec une contraction infinie des longueurs. En réalité, un photon ne peut rien percevoir ou expérimenter, cela se représente en relativité par ce que l’on appelle une géodésique nulle. De son point de vue, il voyage de son point de création (ou émission) à son point de destruction (ou d’absorption) instantanément, puisqu’aucune notion de temps n’existe.

En d’autres mots, seules ces deux interactions (création et destruction) n’ont de sens pour un photon, toutes les autres interactions ne sont pas considérées. C’est pourquoi les calculs en relativité sont effectués dans un référentiel galiléen (ou inertiel). Il est ainsi possible de calculer un blueshift ou un redshift pour un photon dans un référentiel se déplaçant à une vitesse inférieure à c, mais non dans le référentiel du photon. Il en va de même lorsqu’il s’agit de calculer la distance entre son point d’émission et d’absorption.

C’est pourquoi toutes les particules se déplaçant à c n’ont pas de masse au repos. Car une masse au repos est requise pour évoluer dans un référentiel galiléen : la masse et la façon dont est distribuée cette masse donne la définition de l’inertie. Un photon ne peut donc rien percevoir de l’Univers, car cela signifierait interagir avec d’autres particules, ces interactions n’ayant lieu qu’une fois le voyage du photon terminé.