La fusion de trous noirs entraîne-t-elle une perte d’information ?

En 1976, suite à ses travaux sur les trous noirs, Stephen Hawking soulève un paradoxe : selon la relativité générale, l’information absorbée par un trou noir est perdue quand celui-ci s’évapore. Or, les lois de la mécanique quantique imposent une conservation de l’information. De la même manière, quand deux trous noirs fusionnent, ils perdent une partie de leur masse totale. Ce phénomène conduit-il aussi dès lors à une perte d’information ?

Lors des dix fusions de trous noirs détectées par les interféromètres LIGO et Virgo au cours des deux dernières années, chacun des trous noirs impliqués a perdu une fraction de masse totale au cours du processus, aux alentours de 5% en moyenne. Si l’information est encodée dans la masse des trous noirs, celle-ci devrait alors être perdue.

C’est en tout cas ce qu’affirme la relativité générale. Lorsqu’une particule tombe dans un trou noir, toutes ses propriétés — nombre baryonique, nombre leptonique, isospin, etc — ne jouent plus aucun rôle dans la physique du trou noir. L’information relative à ces propriétés est censée être perdue. En d’autres termes, selon la théorie d’Einstein, l’entropie d’un trou noir est nulle.

Trou noir et entropie : une information stockée sur l’horizon des événements

Cependant, cette considération entre en opposition avec les lois de la thermodynamique et de la mécanique quantique. Tout objet ayant une température, une énergie et des propriétés physiques définies possède une entropie non-nulle, et celle-ci ne peut jamais diminuer. Si la matière dont le trou noir provient possède une entropie non-nulle, alors jeter de la matière dans ce dernier ne ferait qu’augmenter son entropie. Le trou noir doit donc posséder une entropie finie, positive et non-nulle.

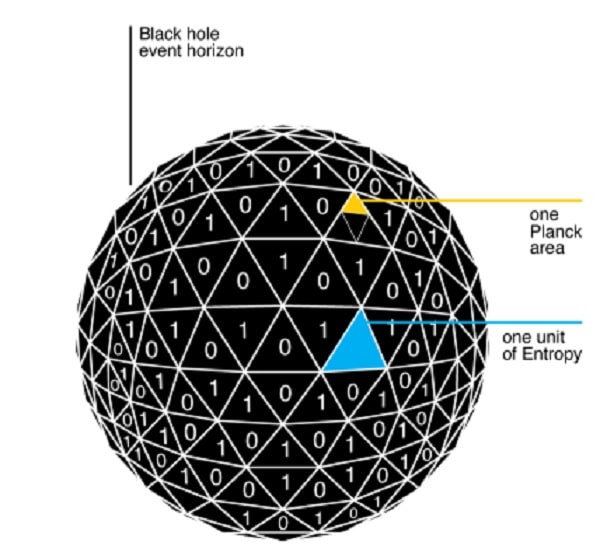
Selon ces règles, toutes les propriétés d’une particule (spin, charge, masse, polarisation, etc) tombant dans un trou noir constituent une information qui doit donc être stockée quelque part. S’il ne s’agit pas de la singularité, alors c’est à un autre endroit. Et c’est le physicien John Wheeler qui est le premier à suggérer que cette information pourrait être stockée sur l’horizon des événements.

Sur le même sujet : Comment les ondes gravitationnelles s’échappent-elles des trous noirs ?

Selon la formule du rayon de Schwarzschild Rs = 2GM/c², c’est la masse d’un trou noir qui détermine la taille de son horizon des événements. Il est donc naturel de penser que l’entropie puisse effectivement se situer sur la surface de cet horizon.

Quand la masse d’un trou noir augmente, son horizon des événements s’agrandit, stockant l’entropie/l’information additionnelle absorbée. Selon les travaux de Jakob Bekenstein et Stephen Hawking, cette information serait encodée sous forme de qubits dans des aires de Planck.

Le devenir de l’information lors de la fusion de deux trous noirs

Lors de la fusion de deux trous noirs, la masse du trou noir résultant équivaut à la somme de la masse des deux trous noirs, diminuée de 10% (5% de masse perdue pour chacun des objets). Ainsi, si chaque trou noir possède une masse de 1 M, le trou noir final aura une masse de 1.9 M. Cela signifie que, simultanément, des ondes gravitationnelles sont émises et transportent une énergie de 0.1 Mc².

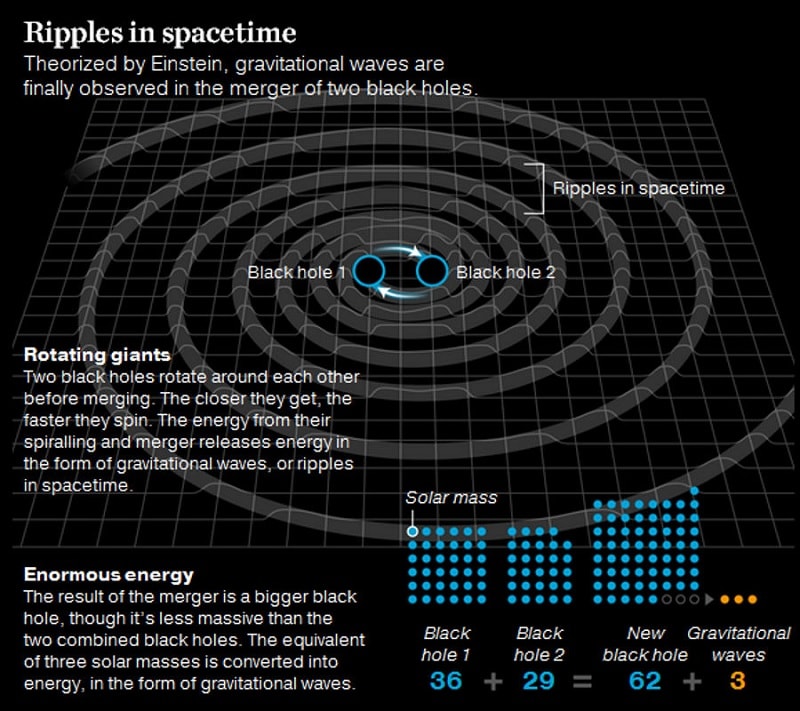
À partir de ce constat, trois scénarios sont possibles :

• l’information des deux trous noirs initiaux reste entièrement encodée sur l’horizon des événements du trou noir final, les ondes gravitationnelles n’en transportent donc pas
• la majorité de l’information se retrouve encodée dans les ondes gravitationnelles, le trou noir final n’en gardant qu’une très petite quantité
• l’information est partagée plus ou moins également entre les ondes gravitationnelles et le trou noir final

L’entropie d’un trou noir est proportionnelle à l’aire de la surface de son horizon des événements, cette dernière étant elle-même proportionnelle à la masse au carré. Cela signifie que si deux trous noirs initiaux ont une entropie de S, alors un trou noir final de 1.9 fois la masse des deux trous noirs possède une entropie de 3.6 S, ce qui est nettement suffisant pour stocker l’information des trous noirs initiaux. C’est le postulat de l’entropie de Bekenstein-Hawking.

Néanmoins, les ondes gravitationnelles doivent transporter une partie de cette information. En effet, elles sont générées par les changements imprimés à la géométrie de l’espace-temps lors de la fusion, et leur énergie provient du changement de distribution de matière-énergie de l’espace-temps. Toutefois, sans théorie de la gravité quantique effective, il est impossible de déterminer quelle quantité d’information est conservée par le trou noir final et quelle quantité est transférée aux ondes gravitationnelles.

Dans tous les cas, lors de la fusion de deux trous noirs, il n’y a aucune perte d’information, étant donné que l’entropie de l’état final est plus élevée que celle de l’état initial. Mais il n’existe actuellement aucune manière d’extraire la quantité d’entropie ou d’information des ondes gravitationnelles ou de l’horizon des événements d’un trou noir. Seule la théorie est ici capable d’apporter quelques éléments d’information.