Apparus en Europe au 10e siècle, les échecs — dont l’origine exacte reste inconnue — sont un jeu de stratégie combinatoire abstrait qui fait appel à d’importantes capacités de réflexion et d’anticipation. Depuis son existence, le jeu a inspiré des centaines de milliers de problèmes mathématiques très complexes, auxquels s’attaquent les plus grands théoriciens du monde. L’un de ces problèmes, connu sous le nom de « problème des n-dames » a été imaginé en 1850. Le mathématicien Michael Simkin, de l’Université de Harvard dans le Massachusetts, propose aujourd’hui une solution.
Sur un plateau d’échecs, la dame est la pièce la plus puissante : c’est la seule pièce qui peut se déplacer dans toutes les directions et de n’importe quel nombre de cases. Le problème des n-dames est le suivant : considérant un nombre n de dames sur un plateau d’échecs de n x n cases, combien existe-t-il de configurations dans lesquelles chaque dame est suffisamment éloignée de ses homologues pour qu’aucune ne puisse prendre les autres ? La solution doit bien entendu respecter les règles de déplacement du jeu.
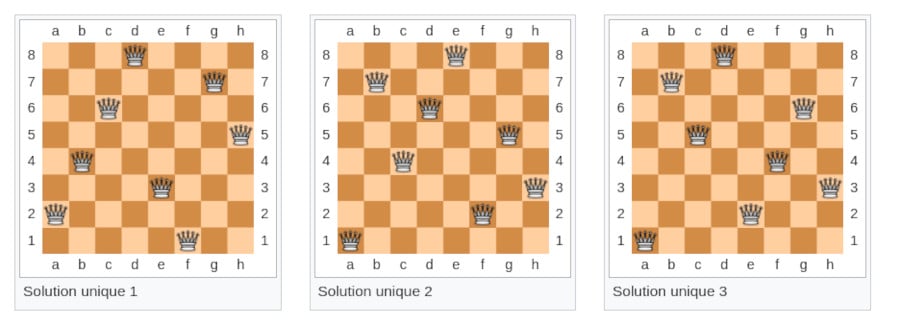
Ce problème est très souvent pris en exemple en informatique pour illustrer des techniques de programmation ; dans ce cas, on considère que n = 8, sur un plateau standard de 64 cases, ce qui mène à 92 solutions distinctes dans lesquelles aucune dame ne partage la même rangée, colonne ou diagonale avec une autre — le nombre de solutions est néanmoins réduit à 12 si l’on écarte les solutions obtenues par rotation ou réflexion d’une autre. Pour un nombre n beaucoup plus grand (1000, 10 000, voire un million de dames), sur un échiquier tout aussi grand, le problème devient tout de suite plus complexe. Mais Michael Simkin du Center of Mathematical Sciences and Applications, apporte aujourd’hui une solution au problème.
Un « simple » problème d’optimisation
Selon lui, il existe environ (0,143 x n)n façons de positionner les dames sur un échiquier de n x n cases pour qu’aucune ne puisse en prendre une autre. Toutefois, ce calcul n’apporte pas la réponse exacte, mais le chiffre « est aussi proche du nombre réel que ce qu’il est possible d’obtenir en ce moment », précise le communiqué de l’Université d’Harvard. Le nombre 0,143 représente en réalité le niveau moyen d’incertitude du résultat.
Comment le mathématicien est-il parvenu à résoudre ce problème vieux de plus de 150 ans ? Cela fait près de 5 ans que Simkin s’intéresse au problème des n-dames, car cela lui permettait d’appliquer les avancées réalisées dans son domaine de prédilection, l’analyse combinatoire — un domaine de recherche axé sur le comptage et les problèmes de sélection et d’arrangement. Il y a quatre ans, il a collaboré avec le mathématicien et expert en échecs Zur Luria, de l’Institut fédéral suisse de technologie de Zurich, pour tenter de résoudre le célèbre problème. Tous deux ont développé de nouvelles techniques, qui les ont menés, après deux ans de travail, à une limite inférieure plus précise de la solution.
En 2020, alors qu’il commence à travailler à l’Université d’Harvard, il décide de se réattaquer au problème sous un autre angle : il explique qu’il s’est intéressé au problème sous-jacent, à savoir la probabilité de présence des dames sur chaque zone de l’immense échiquier. En d’autres termes, il s’est concentré sur les zones de l’échiquier (le centre, les bords, etc.) qui avaient le plus de chances d’être occupées, plutôt que d’accorder le même poids à chaque section de l’échiquier.
Des positions plus favorables que d’autres
En effet, il se trouve que la répartition a son importance : une dame située dans un coin du plateau n’a évidemment pas autant de possibilités d’attaque qu’une autre située en plein centre, par exemple. « En termes formels, cela réduit le problème à un problème d’optimisation », a-t-il déclaré. Les travaux du mathématicien montrent qu’à mesure que le nombre de dames augmente, les configurations possibles tendent à positionner les dames davantage sur les côtés du plateau qu’au centre. Des algorithmes mathématiques classiques ont ensuite permis d’obtenir un nombre possible de configurations.
Cette première étape a permis de définir la limite inférieure de la solution au problème, autrement dit, le nombre minimum de configurations possibles. Simkin a ensuite déterminé la limite supérieure – soit le nombre maximum de configurations possibles répondant au problème – grâce à la méthode dite de l’entropie-croisée, une méthode d’optimisation de type Monte-Carlo. Or, le mathématicien a constaté que les deux limites étaient extrêmement proches l’une de l’autre, ce qui signifie que la solution au problème est située entre ces deux bornes, dans un espace relativement restreint.
Selon lui, il est théoriquement possible de se rapprocher d’une solution encore plus exacte, mais il n’a nullement l’intention de se livrer lui-même à cette recherche. « Je pense personnellement en avoir fini avec le problème des n-reines pour un certain temps, non pas parce qu’il n’y a plus rien à faire, mais simplement parce que j’ai rêvé d’échecs et que je suis maintenant prêt à avancer dans ma vie », a-t-il conclu.

