La majorité des personnes n’utilisent jamais les nombres irrationnels dans leur quotidien. Mais des constantes irrationnelles telles que π et √2 — des nombres qui ne peuvent être réduits à une simple fraction — apparaissent fréquemment en science et en ingénierie. Ces chiffres difficiles à manier ont rebuté les mathématiciens depuis les Grecs anciens. En effet, la légende raconte qu’Hippasus a été noyé pour avoir suggéré l’existence d’irrationnels. Toutefois, récemment, un dilemme vieux de près de 80 ans sur la qualité de leur approximation a été résolu.
Beaucoup de gens conceptualisent les nombres irrationnels en les arrondissant à des fractions ou des nombres décimaux : l’estimation de π comme 3.14, ce qui équivaut à 157/50, conduit à une célébration généralisée de la journée Pi le 14 mars. Pourtant, une approximation différente, 22/7, est plus facile à interpréter et plus proche de π.
Cela soulève la question suivante : existe-t-il une limite à la simplicité et à la précision de ces approximations ? Et pouvons-nous choisir une fraction sous la forme que nous voulons ? En 1941, le physicien Richard Duffin et le mathématicien Albert Schaeffer ont proposé une règle simple pour répondre à ces questions.
Conjecture de Duffin-Schaeffer : une règle pour approximer les fractions
Tout d’abord, décidez du degré de rapprochement de l’approximation pour les fractions d’un dénominateur donné. Rappelez-vous que le « numérateur » fait référence au haut d’une fraction et le « dénominateur » au bas. Ici, toutes les fractions sont entièrement simplifiées. Ainsi, par exemple, 2/4 ne compte pas comme ayant le dénominateur 4 car elle se simplifie en 1/2.
Vous pouvez décider que des fractions simplifiées de la forme n/2 peuvent se rapprocher de tout nombre irrationnel dont la valeur réelle est inférieure à 1/10, donnant à l’approximation une erreur de 1/10. Les fractions qui ressemblent à n/10 sont plus proches les unes des autres sur la droite numérique que celles ayant le dénominateur 2 ; vous pouvez donc limiter l’erreur à 1/100 dans ce cas.
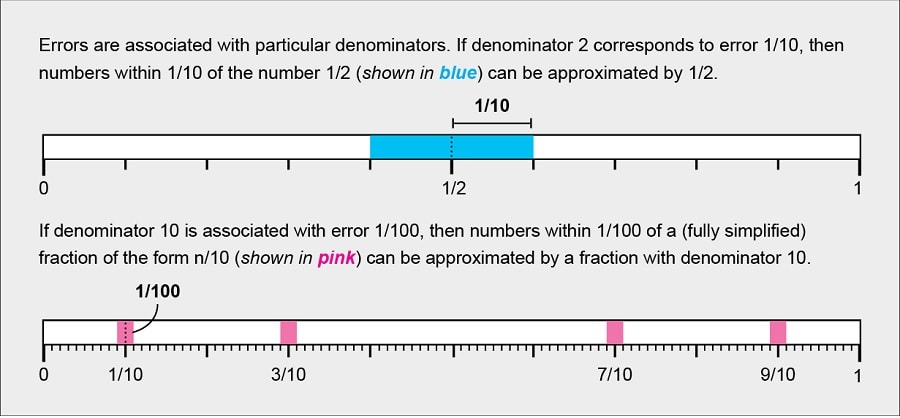
Habituellement, les grands dénominateurs sont associés à des erreurs plus petites. Si cela est vrai et qu’il existe une infinité de dénominateurs que l’on peut utiliser pour approcher un nombre dans les limites de l’erreur correspondante, alors en augmentant le dénominateur, l’approximation peut être améliorée. La règle de Duffin et Schaeffer détermine quand cela peut être fait en fonction de la taille des erreurs.
Si les erreurs choisies sont suffisamment petites dans l’ensemble, un nombre irrationnel x choisi au hasard n’aura qu’un nombre limité d’approximations correctes : il pourrait tomber dans les écarts entre les approximations ayant des dénominateurs particuliers. Mais si les erreurs sont suffisamment importantes, il y aura une infinité de dénominateurs qui créeront une bonne fraction approximative. Dans ce cas, si les erreurs diminuent également à mesure que les dénominateurs s’agrandissent, vous pouvez choisir une approximation aussi précise que vous le souhaitez.
Une conjecture non-prouvée pendant plus de 80 ans
Le résultat est que vous pouvez approximer soit presque tous les nombres ou soit presque aucun. « La dichotomie est frappante » explique Dimitris Koukoulopoulos, mathématicien à l’Université de Montréal. De plus, vous pouvez choisir les erreurs à votre guise, et tant qu’elles sont suffisamment grandes, la plupart des nombres peuvent être approchés à l’infini de multiples façons. Cela signifie qu’en choisissant certaines erreurs à zéro, vous pouvez limiter les approximations à des types de fractions spécifiques, par exemple celles dont les dénominateurs ne sont que des puissances de 10.
Bien qu’il semble logique que de petites erreurs rendent difficile l’approximation des chiffres, Duffin et Schaeffer n’ont pas été en mesure de prouver leur conjecture — et personne d’autre ne l’a été. La preuve est restée « un problème ouvert déterminant » dans la théorie des nombres, explique Christoph Aistleitner, mathématicien à l’Université de technologie de Graz en Autriche, qui a étudié le problème. Jusqu’à cet été, où Koukoulopoulos et James Maynard ont annoncé leur solution dans un article posté sur le serveur de pré-publication arXiv.
La conjecture de Duffin-Schaeffer « a cette simplicité magique dans un domaine des maths qui est normalement exceptionnellement difficile et compliqué » déclare Maynard, professeur à l’Université d’Oxford. Il est tombé par hasard sur le problème — il est théoricien des nombres, mais pas dans le même domaine que la plupart des experts de Duffin-Schaeffer. (Il étudie normalement les nombres premiers — ceux qui ne sont divisibles que par eux-mêmes et 1).
Un professeur de l’Université de York a suggéré à Maynard de s’attaquer à la conjecture de Duffin-Schaeffer après avoir donné une conférence. « Je pense qu’il avait l’intuition qu’il pourrait être bénéfique de placer quelqu’un légèrement en dehors de ce domaine immédiat » indique Maynard. Cette intuition s’est avérée juste, même si elle ne porterait pas ses fruits avant plusieurs années. Longtemps après cette conversation initiale, Maynard a suggéré à Koukoulopoulos de collaborer.
Sur le même sujet : Deux mathématiciens trouvent la “solution” à la grande question sur « la vie, l’univers et le reste »
Colorer les nombres pour mieux matérialiser le problème
Maynard et Koukoulopoulos savaient que des travaux antérieurs avaient réduit le problème à un facteur concernant les facteurs premiers des dénominateurs, à savoir les nombres premiers qui, multipliés ensemble, donnent le dénominateur. Maynard a suggéré de penser au problème en colorant les nombres : « Imaginez, sur la droite des nombres, colorer tous les nombres proches des fractions de dénominateur 100 ». La conjecture de Duffin-Schaeffer dit que si les erreurs sont suffisamment grandes et qu’on le fait à chaque fois pour tous les dénominateurs possibles, presque tous les chiffres seront colorés à l’infini.
Pour un dénominateur particulier, seule une partie de la droite numérique sera colorée. Si les mathématiciens pouvaient montrer que pour chaque dénominateur, des zones suffisamment différentes étaient colorées, elles garantiraient que presque chaque nombre le serait. S’ils pouvaient également prouver que ces sections se chevauchaient, ils pourraient conclure que cela s’est produit plusieurs fois. Une façon de saisir cette idée de zones différentes, mais qui se chevauchent, est de prouver que les régions colorées par des dénominateurs différents n’ont rien à faire entre elles — elles sont indépendantes.
Mais ce n’est pas totalement vrai, surtout si deux dénominateurs partagent de nombreux facteurs premiers. Par exemple, les dénominateurs possibles 10 et 100 partagent les facteurs 2 et 5, et les nombres pouvant être approximés par des fractions de la forme n/10 présentent des chevauchements frustrants avec ceux pouvant être approchés par des fractions n/100.
Une solution mise en évidence à l’aide des graphes
Maynard et Koukoulopoulos ont résolu cette énigme en recadrant le problème en termes de réseaux que les mathématiciens appellent graphes. Les points dans leurs graphiques représentent les dénominateurs possibles que les chercheurs ont voulu utiliser pour la fraction approximative, et deux points sont reliés par une arête s’ils ont beaucoup de facteurs premiers en commun. Les graphiques ont beaucoup d’arêtes précisément dans les cas où les dénominateurs autorisés ont des inter-dépendances.
L’utilisation de graphiques a permis aux deux mathématiciens de visualiser le problème d’une nouvelle manière. « L’une des idées les plus importantes dont vous avez besoin est d’oublier tous les aspects sans importance du problème et de vous concentrer sur un ou deux facteurs qui le rendent très spécial » déclare Maynard.
Utiliser des graphes « non seulement vous permet de prouver le résultat, mais il vous dit vraiment quelque chose de structurel à propos de ce qui se passe dans le problème » ajoute-t-il. Maynard et Koukoulopoulos en ont déduit que les graphes avec de nombreuses arêtes correspondaient à une situation mathématique très structurée particulière, qu’ils pouvaient analyser séparément.
La solution du duo a été une surprise pour beaucoup dans le domaine. « Le sentiment général était que cela n’était pas près d’être résolu » indique Aistleitner. « La technique consistant à utiliser des graphiques est peut-être considérée à l’avenir comme tout aussi importante, voire peut-être plus importante encore que la conjecture de Duffin-Schaeffer actuelle » déclare Jeffrey Vaaler, professeur à la retraite à l’université de Londres.