Quelle est la forme des trous noirs ?

Trous noirs : une forme due à leur calvitie

Les trous noirs peuvent donc être en rotation ou non, et être chargés ou non. Il est ainsi possible de les classer. C’est ce qu’ont fait les physiciens Brandon Carter, Stephen Hawking et Werner Israel dans les années 1970 en démontrant qu’un trou noir ne peut être décrit que par trois paramètres : sa masse (M), son moment cinétique (J) et sa charge électrique (Q).

Quel que soit son mode de formation ou le corps qui en est à l’origine, un trou noir ne sera toujours décrit que par ces trois propriétés. Ce théorème est nommé « théorème de la calvitie » car toutes les informations spécifiques — assimilées ici à des « cheveux » — concernant la matière ayant permis la formation du trou noir sont irrémédiablement perdues une fois le trou noir formé ; il est ainsi impossible de remonter jusqu’à l’étoile progénitrice.

Selon le théorème de la calvitie, il existe donc quatre types de trou noir :

• • • trou noir de Schwarzschild, avec M ≠ 0, J = 0 et Q = 0
    • trou noir de Reissner-Nordström, avec M ≠ 0, J = 0 et Q ≠ 0
    • trou noir de Kerr, avec M ≠ 0, J ≠ 0 et Q = 0
    • trou noir de Kerr Newman, avec M ≠ 0, J ≠ 0 et Q ≠ 0

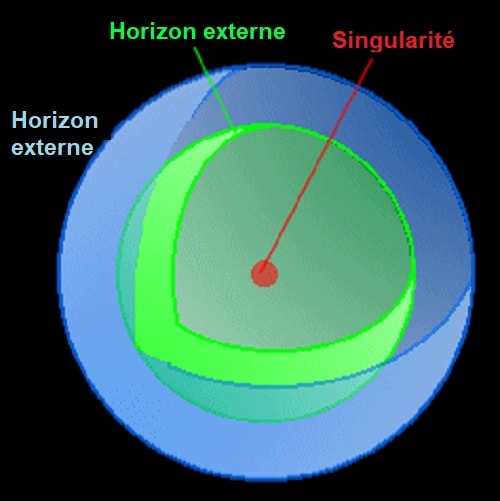
Les trous noirs de rotation nulle possèdent simplement un horizon des événements sphérique. Ils apparaissent donc comme une sphère au sein d’un espace à 4 dimensions (3+1). En réalité, il est d’usage de décomposer l’horizon d’un trou noir en un horizon interne et un horizon externe, définis par leur distance à la singularité centrale. Dans le cas des trous noirs de rotation nulle, les deux horizons sont identiquement sphériques.

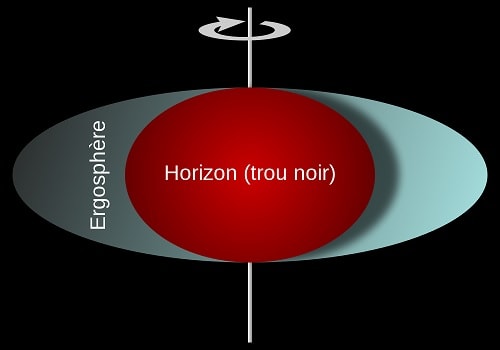
Quant aux trous noirs de rotation non-nulle, ils diffèrent de leurs homologues statiques par la présence d’une seconde région appelée « ergosphère ». Il s’agit de la région en rotation autour du trou noir dans laquelle l’espace-temps, ainsi que toute particule, est entraîné dans le mouvement d’ensemble de rotation du trou noir. Cet phénomène d’entraînement s’appelle l’effet Lense-Thirring. En 2011, le satellite Gravity Probe B a confirmé l’existence de cet effet autour d’un trou noir.

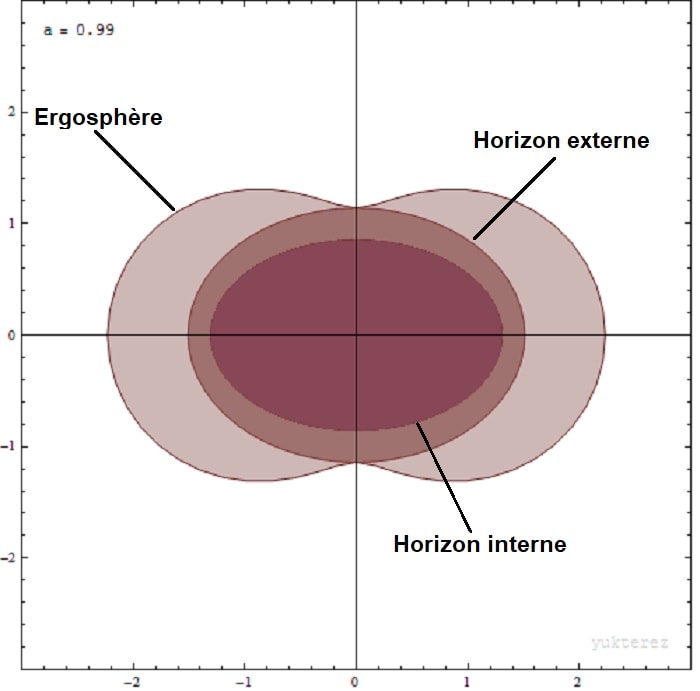
Les trous noirs en rotation possèdent donc une structure différente, la présence de l’ergosphère se rajoutant à celle de l’horizon des événements. L’ergosphère, du fait du mouvement de rotation rapide dont elle est le siège, possède une forme de sphéroïde oblate dont le petit axe est aligné avec l’axe de rotation du trou noir. Quant à l’horizon des événements, il est également sphéroïde, mais bien moins aplati que l’ergosphère.

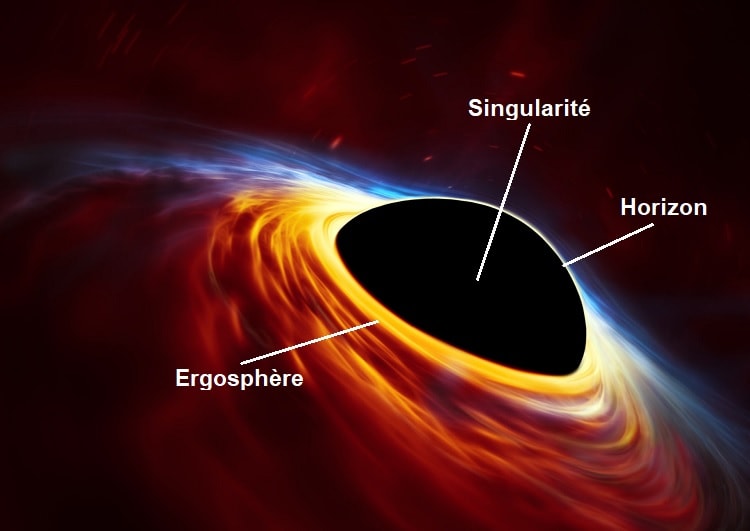
Le théorème de la calvitie interdit l’existence d’autres géométries car alors plus de trois paramètres seraient nécessaires pour décrire de tels trous noirs. Dans le cas d’un espace-temps à plus de 4 dimensions, des trous noirs de forme cylindrique peuvent exister ; ils sont alors appelés des « cordes noires ». Dans la relativité générale classique, de telles configurations ne peuvent apparaître. Mais dans des théories généralisant la relativité générale à un plus grand nombre de dimensions, des configurations cylindriques stables pourraient apparaître.