Les trous noirs font partie des objets les plus mystérieux du cosmos. Bien que leur existence ne soit aujourd’hui plus débattue au sein de la communauté scientifique, l’impossibilité de les observer directement rend parfois compliquée leur représentation. Notamment, les scientifiques se sont interrogés sur la véritable forme des trous noirs.
Si l’idée de corps dont la vitesse de libération serait plus importante que celle de la lumière dans le vide fait son apparition dès le 18ème siècle, c’est au début du 20ème siècle, avec la relativité générale d’Albert Einstein, qu’elle prend véritablement forme. Après sa première publication en 1915, certains physiciens commencent à trouver des solutions particulières aux équations de la relativité générale, tels que Karl Schwarzschild et Roy Kerr. Ces solutions seront rapidement interprétées comme des solutions de type trou noir (terme qui n’apparaît en France qu’en 1973.
Sur le même sujet :
L’Event Horizon Telescope livre les premiers détails de la structure du trou noir Sagittarius A*
C’est à partir de 1971 que le premier trou noir est détecté grâce à l’observation de l’étoile binaire X à forte masse, Cygnus X-1. Par suite, de très nombreux autres trous noirs seront identifiés. Ces objets ne laissant échapper aucune lumière, il est impossible de pouvoir les observer directement. Les observations sont donc indirectes, et se basent sur la détection du rayonnement électromagnétique émis depuis le disque d’accrétion (disque de gaz et poussières en rotation autour du trou noir) ou lors d’un jet relativiste polaire, sur les perturbations gravitationnelles et sur les ondes gravitationnelles.
Trous noirs et autres objets célestes : une forme commune ?
La question de la forme des trous noirs se pose naturellement lorsque l’on considère la forme des autres corps célestes visibles. Dans l’Univers, et à moins d’une collision ou d’une origine autre qu’un effondrement gravitationnel ou une accrétion, les corps sont globalement sphériques. En effet, la gravité s’exerçant avec la même intensité dans toutes les directions, lors de sa formation, un objet prend naturellement une forme sphérique.
Cependant, il ne s’agit pas d’une sphéricité parfaite ; d’autres paramètres tels que la masse, le champ magnétique ou la rotation, jouent un rôle et confèrent généralement à l’objet une forme de sphéroïde. Cet effet est d’autant plus prononcé lorsque le corps est en rotation rapide, résultant en un aplatissement des pôles et tendant ainsi vers une géométrie sphéroïde oblongue. Dès lors, un trou noir répond-il à cette situation de la même manière ?
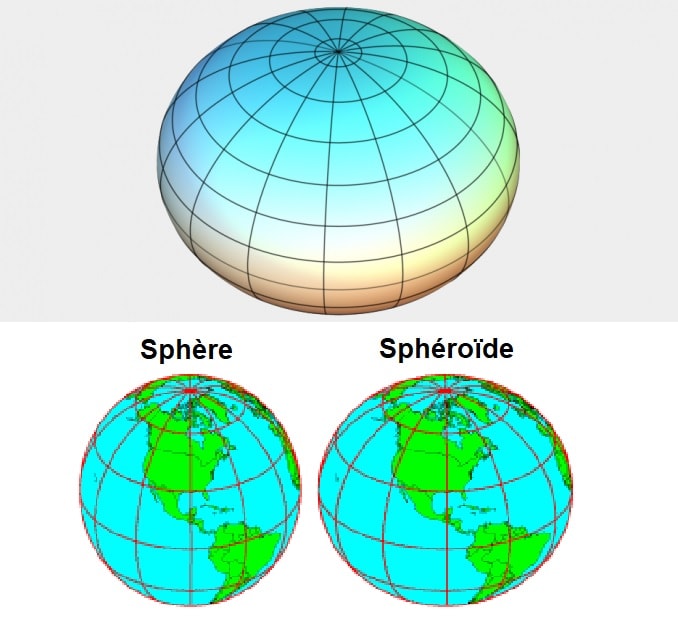
La question est légitime dans le sens où le mécanisme de formation le plus simple d’un trou noir est celui de l’effondrement gravitationnel d’un corps massif. Il pourrait donc exister une connexion directe potentielle entre la forme du corps effondré et la forme du trou noir. Généralement, les trous noirs sont considérés comme sphériques.
Et si un corps massif non sphérique venait à s’effondrer, quel serait le résultat ? Pour les physiciens, deux réponses possibles. La première suggère que toute caractéristique non sphérique du corps est « perdue » lors de l’effondrement gravitationnel. La seconde suggère que l’effondrement d’un corps non sphérique n’aboutirait pas à un trou noir mais à une singularité nue ou à toute autre configuration compacte.
La structure physique des trous noirs
C’est en 1916 que Karl Schwarzschild met en évidence une solution exacte aux équations de la relativité générale : la métrique de Schwarzschild. Il s’agit d’une valeur du tenseur métrique pour une distribution de matière immobile, sphérique, de rotation nulle et de charge électrique nulle. Cette configuration particulière de l’espace-temps correspond ainsi au trou noir de Schwarzschild.
Trois notions apparaissent dès lors avec cette première solution : l’horizon des événements — la région du trou noir à partir de laquelle la vitesse de libération devient supérieure à la vitesse de la lumière dans le vide. La singularité gravitationnelle — une zone de l’espace-temps au centre du trou noir au voisinage de laquelle le champ gravitationnel diverge (tend vers l’infini). Le rayon de Schwarzschild — le rayon de l’horizon d’un trou noir.
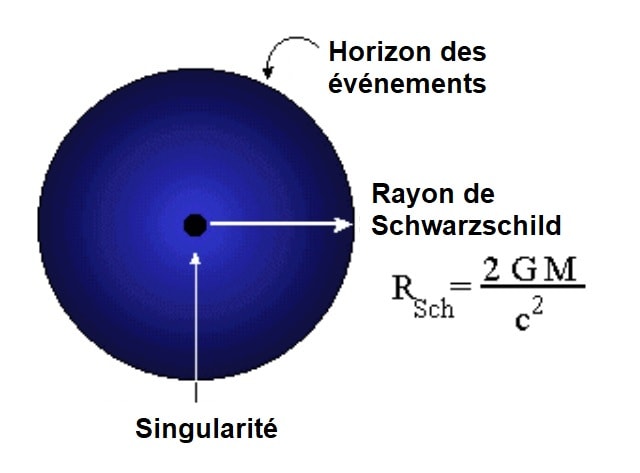
Ce dernier est important car il permet d’établir la première condition de formation des trous noirs : pour qu’un trou noir se forme, le rayon de distribution de masse de l’objet doit être inférieur au rayon de Schwarzschild. Dès lors, suite à l’effondrement gravitationnel, un horizon sphérique de rayon égal au rayon de Schwarzschild se forme. C’est donc principalement l’apparition d’un horizon des événements qui définit un trou noir. Cette solution confère donc une géométrie sphérique aux trous noirs.
En 1917, les physiciens Hans Reissner et Gunnar Nordström généralisent la métrique de Schwarzschild pour des trous noirs sphériques, chargés et de rotation nulle au sein de la métrique de Reissner-Nordström. Il faut attendre 1963 pour que le physicien Roy Kerr généralise la solution de Schwarzschild à des trous noirs quasi sphériques, non chargés et en rotation via la métrique de Kerr.

En 1965, avec le physicien Ezra Newman, Kerr étend cette solution à des trous noirs chargés en rotation ; c’est la métrique de Kerr Newman. Les travaux de Kerr sont importants car avec un moment cinétique (rotation) non-nul, la structure des trous noirs est modifiée. Tous les trous noirs astrophysiques sont réputés être des trous noirs de Kerr car, pour obtenir un trou noir de Schwarzschild, l’hypothèse, peu réaliste, d’une étoile progénitrice de rotation et charge nulles serait nécessaire.
Trous noirs : une forme due à leur calvitie
Les trous noirs peuvent donc être… (suite à la page suivante)



 Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]
Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]