Décédé le 14 mars 2018 à l’âge de 76 ans, le grand physicien Stephen Hawking aura laissé un riche héritage dans le domaine de la physique théorique. Ayant notamment révolutionné la physique des trous noirs, le professeur de Cambridge faisait part, il y a quelques années, de son désir qu’une formule emblématique, dont il est l’auteur, soit gravée sur sa pierre tombale : l’entropie d’un trou noir.
Lors de l’anniversaire de ses 60 ans, au cours d’une conférence donnée sur le futur de la physique théorique et de la cosmologie, le défunt cosmologiste avait captivé son auditoire en affirmant qu’il souhaite que sa célèbre formule décrivant l’entropie des trous noirs soit gravée sur sa pierre tombale.
Les trous noirs représentent le sujet d’étude central de la carrière scientifique de Stephen Hawking. Au début de ses travaux, le physicien est amené à calculer les quantités d’énergie en jeu lors de la collision de deux trous noirs. Sachant que lors d’un tel événement, une quantité non-négligeable d’énergie est rayonnée sous forme d’ondes gravitationnelles, Hawking cherche à savoir quelle quantité d’énergie peut être collectée à partir du flux d’ondes gravitationnelles.
Le résultat qu’il obtient est surprenant : lors de la collision et de la fusion de deux trous noirs, le trou noir final possède une surface supérieure à la somme des surfaces des deux trous noirs initiaux. Hawking fait alors un premier rapprochement entre le second principe de la thermodynamique affirmant que l’entropie d’une système croît au cours du temps, et la surface d’un trou noir ; un trou noir pourrait donc posséder une entropie proportionnelle à sa surface.
Cependant, deux problèmes se posent alors au cosmologiste. Le premier est que tout objet auquel l’on associe une entropie doit posséder une température. Et le second, extension du premier, est que tout objet possédant une température non-nulle émet un rayonnement. Or, dans les modèles théoriques, les trous noirs n’émettent absolument aucun rayonnement. Dès lors le physicien est confronté à une barrière l’empêchant d’appliquer les principes thermodynamiques aux trous noirs.
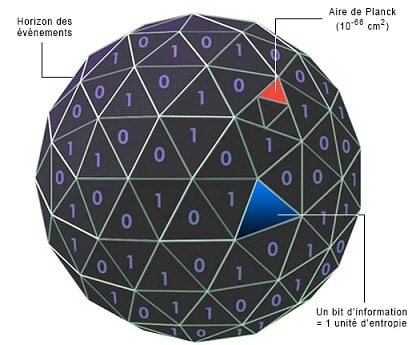
Il faut attendre les travaux du physicien israélo-mexicain Jacob Bekenstein pour que la situation se débloque. À l’aide d’élégants calculs, Bekenstein détermine qu’à chaque fois qu’une particule est absorbée par un trou noir, la surface de se dernier augmente d’1/4 de la surface de Planck (une aire de Planck). Il montre qu’il est alors possible de décomposer la surface d’un trou noir en surfaces de Planck, elles-mêmes décomposées en aires de Planck, chacune pouvant contenir 1 bit d’information. Le nombre de bits devient ainsi proportionnel à la surface du trou noir.
Il suffit de lire la surface du trou noir pour mesurer la quantité d’informations absorbée par celui-ci. Et puisque l’entropie désigne également la quantité maximale d’information qui peut être stockée par un objet, les physiciens peuvent de nouveau raccorder la thermodynamique aux trous noirs. Mais la question de la température se pose toujours.
C’est Hawking, en 1974, qui en apporte la solution théorique. Il montre que, via les fluctuations quantiques du vide, un trou noir rayonne à la manière d’un corps noir, et que la température de ce rayonnement est proportionnelle à la gravité de surface du trou noir. Grâce au processus du rayonnement de Hawking et à la mise en évidence d’une température, le cosmologiste parvient alors à déterminer l’équation de l’entropie d’un trou noir ; entropie proportionnelle à la surface du trou noir (son horizon des événements).
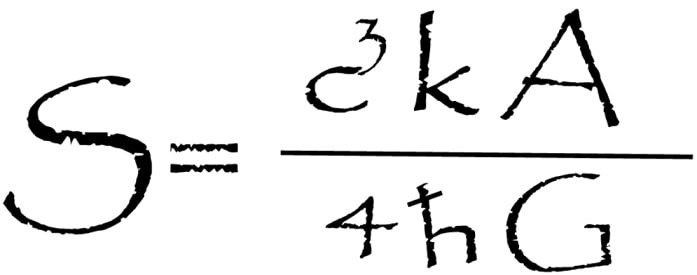
Cette formule porte le nom de « formule de Bekenstein-Hawking » et a totalement révolutionné les modèles théoriques en les obligeant à dorénavant considérer une réelle thermodynamique des trous noirs. À partir de ces travaux, Hawking a également proposé l’hypothèse qu’à l’image des trous noirs, toute l’information de notre univers soit contenue à sa surface, c’est-à-dire sur une sorte d’horizon des événements cosmologique. Le contenu de notre univers ne serait alors que la projection de l’information encodée à sa surface. Cette idée servira de base à la formulation du principe holographique.
Le souhait d’Hawking d’avoir l’équation de l’entropie des trous noirs gravée sur sa pierre tombale est, à bien des égards, légitime au regard de l’histoire de la science. En effet, la tombe de l’auteur de la première formule donnant l’entropie d’un système, le célèbre physicien autrichien Ludwig Boltzmann, est déjà ornée de sa formule. Stephen Hawking a donc gagné, lui aussi, le droit de réfléchir à tout jamais aux mystères du cosmos sous la veille révérencieuse de sa fabuleuse découverte.




 Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]
Un trou noir est un objet compact au champ gravitationnel si intense qu'aucune matière ni aucun rayonnement ne peut s'en échapper. Puisque ces astres n'émettent aucune lumière, ils ne peuvent être... [...]
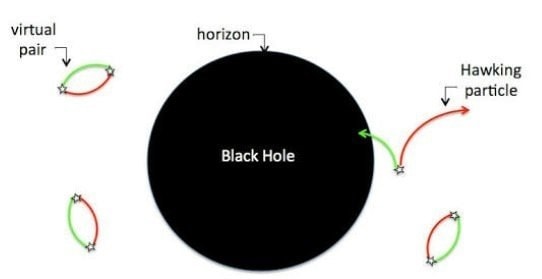 Selon la théorie développée par Stephen Hawking, les trous noirs s'évaporent et ne seraient pas "totalement noirs". Ils seraient légèrement luisants et constamment en train d’émettre des particules par intensité faible depuis leur surface. Il s’agit du rayonnement de Hawking [...].
Selon la théorie développée par Stephen Hawking, les trous noirs s'évaporent et ne seraient pas "totalement noirs". Ils seraient légèrement luisants et constamment en train d’émettre des particules par intensité faible depuis leur surface. Il s’agit du rayonnement de Hawking [...].