En 1915, Albert Einstein publie ses travaux sur la théorie de la relativité générale décrivant la gravitation comme la déformation géométrique d’un espace-temps à 4 dimensions : 3 dimensions spatiales et 1 dimension temporelle. Nous évoluons quotidiennement dans ces quatre dimensions qui nous sont accessibles par l’observation et l’expérimentation. Cependant, certaines théories décrivent un univers à plus de 4 dimensions et admettent ainsi l’existence de dimensions supplémentaires.
Après la publication de la théorie de la relativité générale, le physicien allemand Theodor Kaluza entreprend des travaux sur l’unification de la relativité générale avec l’électromagnétisme. En 1919 il communique ceux-ci à Einstein, qui les accepte, puis les publie en 1921. Les équations de Kaluza à 5 dimensions contiennent 15 composantes : 10 reliées à la géométrie de l’espace-temps à 4 dimensions, 4 reliées aux équations de Maxwell et 1 reliée à un champ scalaire non-identifié appelé « radion ». Kaluza introduit également une condition arbitraire d’isomérie sur la géométrie de l’espace-temps appelée « l’hypothèse du cylindre ».
En 1926, le physicien suédois Oskar Klein formalise la théorie de Kaluza en termes quantiques, notamment en décrivant le radion via l’équation de Klein-Gordon (équation de Schrödinger relativiste). Afin de rendre cohérente l’hypothèse du cylindre, Klein montre que la cinquième dimension introduite par Kaluza doit être enroulée à l’échelle microscopique ; il détermine ainsi que cette dimension supplémentaire aurait la forme d’un cercle, et calcule une valeur de 10-30 cm pour son rayon. Ces travaux porteront par suite le nom de théorie de Kaluza-Klein (ou théorie KK). Dans les années 1940, les équations du champ de Kaluza-Klein seront complétées et, en 2015, ces dernières ont été jugées correctes par un logiciel d’algèbre tensoriel.
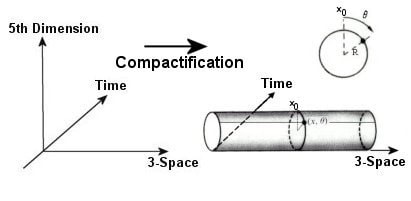
La théorie de Kaluza-Klein est donc la première théorie à décrire un espace-temps possédant une dimension spatiale supplémentaire, soit un univers à 5 dimensions. À partir des années 1970 et sur la base de ces précédents travaux, plusieurs physiciens menés par Gabriele Veneziano commencent à développer une théorie de la gravité quantique unifiant la relativité générale et la mécanique quantique : la théorie des cordes.
Lors de la première formulation de cette théorie, les physiciens s’aperçoivent que les cordes ne peuvent se propager de manière cohérente dans un espace-temps à seulement 4 dimensions. Pour maintenir la cohérence mathématique d’ensemble, des dimensions supplémentaires sont ajoutées. Un peu plus tard, il est démontré que ces dimensions supplémentaires émergent en réalité naturellement du cadre physico-mathématique des cordes.
Ainsi, la première théorie des cordes, la théorie des cordes bosoniques, comportait 26 dimensions. Avec le développement du concept de supersymétrie, la théorie évolue pour devenir la théorie des supercordes. La théorie des cordes bosoniques est abandonnée au profit des supercordes, qui s’avèrent plus élégantes et rigoureuses. Le nombre de dimensions supplémentaires diminue et passe à 6, donnant un espace-temps à 10 dimensions. Ce nombre repasse à 11 avec la théorie M développée par Edward Witten et visant à unifier les 5 théories des supercordes.
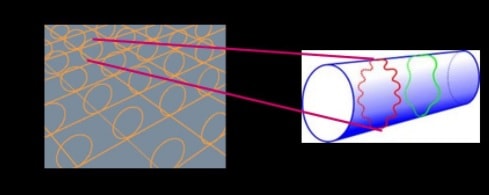
Dans la théorie KK, les dimensions supplémentaires sont enroulées à l’échelle de Planck (10-33 cm) sous forme de cercle, de sphère ou de tore. En théorie des supercordes, ces dimensions ont une géométrie bien plus complexe car elles se trouvent à l’intérieur d’un espace de compactification. Un espace de compactification est un objet géométrique permettant le processus de réduction dimensionnelle, c’est-à-dire le processus visant à réduire un espace de dimension X à un sous-espace de dimension Y, avec Y < X. Par exemple, si l’on prend une théorie des supercordes avec un espace-temps à 10 dimensions, la réduction dimensionnelle réduit cet espace-temps à 4 dimensions, les 6 dimensions supplémentaires étant compactifiées à l’échelle de Planck.
En théorie des supercordes, l’espace de compactification utilisé est appelé « espace de Calabi-Yau » ou « variété de Calabi-Yau », du nom des mathématiciens Eugenio Calabi et Shing-Tung Yau qui en sont à l’origine. Il s’agit d’une variété mathématique particulière – une variété différentielle dite « kählérienne » – qui permet, lorsqu’elle est utilisée comme espace de compactification, de préserver la supersymétrie de la théorie à 10 dimensions lorsque celle-ci est réduite à 4 dimensions. Ainsi, un espace de Calabi-Yau contient 6 dimensions.
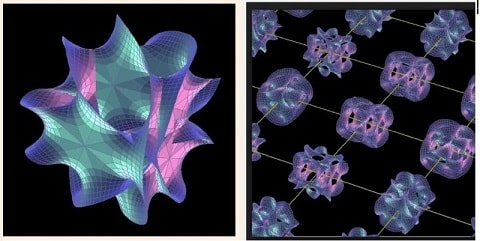
L’apparition des dimensions supplémentaires est également expliquée par la théorie des supercordes. Lors de l’ère de Plank, soit 10-43 secondes après le Big Bang, toutes les dimensions de l’espace-temps sont enroulées à l’échelle de Planck et maintenues compactées par des condensats de supercordes. Puis, lors d’une transition de phase, la brisure de symétrie d’un champ scalaire sous-jacent de la théorie, a permis à 4 dimensions de se libérer et se déplier à la taille de l’univers, tandis que les autres sont restées piégées.
Basées sur les supercordes, d’autres théories prédisent l’existence de dimensions supplémentaires. En 1998, les physiciens Nima Arkani-Hamed, Savas Dimopoulos et Gia Dvali introduisent le modèle ADD proposant l’existence de grandes dimensions supplémentaires (Large Extra Dimensions, LED). Dans cette théorie, l’électromagnétisme et les interactions nucléaires faible et forte sont confinées au sein des 4 dimensions visibles, tandis que la gravité peut se propager au sein de dimensions supplémentaires plus grandes que l’échelle de Planck (de l’ordre du femtomètre pour 6 dimensions).
Ce modèle vise ainsi à solutionner le problème de la hiérarchie, c’est-à-dire expliquer pour quelle raison la gravité est si faible par rapport aux autres interactions élémentaires ; en se propageant dans des dimensions supplémentaires, la gravité subit un effet d’écrantage et se trouve amoindrie dans les 4 dimensions usuelles.
Plusieurs propositions ont été faites dans le but de tester expérimentalement l’existence de dimensions supplémentaires. Dans le cas de dimensions compactifiées à l’échelle de Planck, les niveaux d’énergie accessibles au LHC ne sont pas encore suffisants. En revanche, dans le modèle ADD, les 13 TeV déployés par l’accélérateur de particules pourrait mettre en évidence des dimensions de l’ordre du femtomètre.
Un défaut d’énergie dans le spectre de distribution des produits de collisions proton-proton, s’il était observé, pourrait également constituer un indice de la présence de telles dimensions. En outre, plusieurs études ont démontré la possibilité de détecter ou contraindre la taille des dimensions supplémentaires grâce à des phénomènes cosmologiques comme les ondes gravitationnelles.

