Le phénomène d’intrication quantique est un des mécanismes les plus étudiés par la physique moderne depuis ces dernières années. Bien qu’elle ait fait l’objet de nombreuses expérimentations toujours plus poussées, l’intrication quantique demeure encore un « mystère » aux yeux des physiciens, notamment en ce qu’elle semble contredire le principe de localité.
Lorsque deux systèmes quantiques (deux particules par exemple) sont intriqués, ils ne forment plus qu’un seul système indissociable et unique. Il n’est alors plus possible de décrire individuellement chaque particule ; il n’y a que le système dans son ensemble qui peut être décrit. Lorsqu’une mesure est effectuée sur une particule, l’autre particule est simultanément et instantanément affectée et subit également la mesure.
Cependant, l’intrication ne faisant pas disparaître l’incertitude sur la mesure, et le théorème de non-clonage quantique s’appliquant, le phénomène d’intrication ne permet pas de communiquer à des vitesses supraluminiques. Il n’y a donc, dans ce cas-ci, aucune contradiction entre la relativité restreinte et la mécanique quantique.
La question qui se pose toutefois est la suivante : l’intrication quantique fonctionne-t-elle sur une distance infinie ? Ou est-elle limitée dans l’espace-temps par une distance maximale au terme de laquelle elle finit par se rompre ? Dans une étude publiée le 17 novembre 2017 sur arXiv (1), le physicien Yong Xiao (Collège des Sciences Physiques et Technologiques, Université d’Hebei, Chine) opte pour cette seconde hypothèse et propose une distance maximale à l’intrication.
L’intrication quantique : une distance infinie communément admise
Lorsque la question de la distance spatiale est soulevée concernant l’intrication quantique, la réponse commune est que celle-ci est illimitée. En d’autres termes, l’intrication quantique s’affranchit des contraintes spatio-temporelles et maintient ses effets indifféremment de la distance séparant les deux particules.
Cette considération découle naturellement du fait que dans le cadre de la mécanique quantique et de la relativité restreinte, il est impossible de construire une distance fondamentale à partir de la constante de Planck réduite « ħ », de la vitesse de la lumière « c » et de la longueur d’onde quantique « λ » d’une particule.
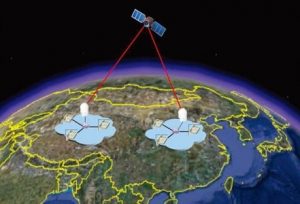
C’est dans le but de tester cette distance que de nombreuses expériences sont menées depuis les années 1970. Progressivement, les scientifiques sont parvenus à réaliser et maintenir des états intriqués sur des échelles spatiales de plus en plus grandes. Récemment (2), via le satellite Micius, une équipe de physiciens a réussi à maintenir un état intriqué sur une distance de 1200 km.
Néanmoins, sur de plus grandes distances (de l’ordre de plusieurs centaines de milliers de kilomètres), il est envisageable que les effets de la gravité et la structure même de l’espace-temps puissent impacter la relation d’intrication entre deux particules, pouvant l’affaiblir, la déstabiliser ou tout simplement la rompre.
En effet, en considérant la constante gravitationnelle G, il est possible de construire une longueur fondamentale, appelée « longueur de Planck » : lp = √ħG/c3 = 1.616×10-35 m. La longueur de Planck constitue la plus petite longueur admissible en mécanique quantique. Combinée à la longueur d’onde quantique « λ » des particules intriquées, une autre longueur peut être construite :
LQE = λαlp1-α
Si sur de très grandes distances, l’intrication quantique est affectée par des effets gravitationnels quantiques, imposant dès lors une distance maximale au-delà de laquelle elle se rompt, cette distance maximale prend nécessairement la forme de cette équation. La seule inconnue réside alors dans la valeur du coefficient « α », qui peut être égale à 2 ou à 3.
Situation dans laquelle α = 2 : les contraintes d’énergie en théorie quantique des champs
La théorie quantique des champs (QFT) est la théorie quantique décrivant la dynamique des champs quantiques du Modèle Standard. Dans ce cadre, les particules élémentaires sont décrites comme des excitations des champs quantiques qui leur sont associés. Cependant, le formalisme quantique utilisé pour élaborer la QFT n’est qu’une approximation de celle-ci, à basse énergie.
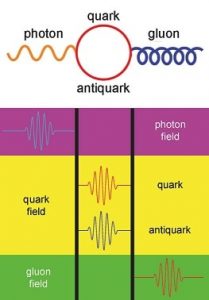
En d’autres termes, pour des seuils d’énergies élevés, la QFT est… (suite à la page suivante)