Qu’est-ce qu’une singularité gravitationnelle ?

En 1915, le physicien Albert Einstein publie ses travaux sur la relativité générale. Pour la première fois, la gravitation n’est plus traitée comme une force exercée entre deux corps selon la conception newtonienne, mais comme la déformation de l’espace-temps en présence d’énergie. Lorsque les phénomènes gravitationnels deviennent extrêmes, l’espace-temps peut donner lieu à l’émergence de singularités gravitationnelles.

L’équation d’Einstein, encore appelée équation du champ gravitationnel, est le socle mathématique de la relativité générale. Elle relie la courbure de l’espace-temps à la distribution masse-énergie. Ainsi, la structure géométrique de l’espace-temps est directement reliée au tenseur énergie-impulsion (outil mathématique décrivant la répartition masse-énergie dans l’espace-temps). Malgré la grande complexité de ces équations aux dérivées partielles non linéaires, la recherche de solutions à celles-ci est importante en cosmologie.

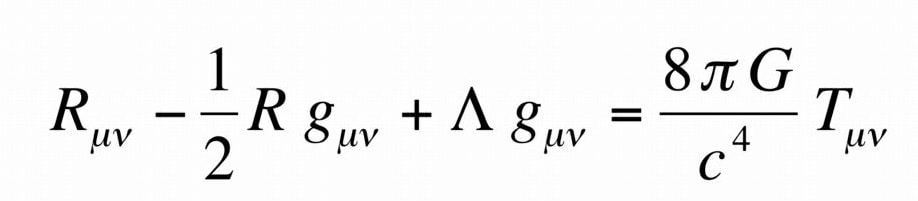
En effet, les solutions à l’équation du champ correspondent aux différentes valeurs que peut prendre le tenseur métrique g_µv ; ce dernier est le tenseur décrivant la géométrie de l’espace-temps (longueurs et angles principalement). Ces solutions sont donc appelées des « métriques ». Plusieurs métriques, correspondant à des configurations spatio-temporelles différentes, ont déjà été mises en évidence depuis 1915 : la métrique de Minkowski décrivant un espace-temps vide de matière et d’énergie, la métrique de Schwarzschild décrivant l’espace-temps autour d’une distribution sphérique de masse-énergie (trou noir statique par exemple), la métrique FLRW (Friedmann-Lemaître-Robertson-Walker) décrivant un espace-temps homogène et isotrope en expansion, etc.

Cependant, la résolution des équations du champ ne donne pas toujours des solutions exactes ou approchées. Dans certaines conditions, impliquant des phénomènes gravitationnels particulièrement extrêmes, l’équation d’Einstein amène à des solutions indéfinies ; plus précisément, l’objet mathématique qui émerge de ce contexte particulier est impossible à définir. Une telle « indéfinition » mathématique est appelée une « singularité ». Ces situations où la géométrie de l’espace-temps est indéfinie sont le centre des trous noirs et le point d’origine de l’univers.

À la fin des années 1960, les physiciens britanniques Stephen Hawking et Roger Penrose se penchent sur le problème des singularités dans le cadre de la relativité générale. Dans l’impossibilité d’effectuer des simulations numériques pour déterminer l’évolution concrète d’un astre massif en effondrement gravitationnel, les deux physiciens énoncent, à partir des équations du champ, un certain nombre de conditions nécessaires à l’apparition d’une singularité gravitationnelle. Ces « règles » donneront naissance au théorème sur les singularités.

Parmi ces conditions se trouvent la nécessité d’une gravitation attractive et donc d’une pression positive à haute densité (une pression négative au cœur des étoiles serait « éliminatoire ») ainsi que l’existence d’une dépendance entre le champ gravitationnel et la géométrie de l’espace-temps. Ces pré-requis très généraux s’adaptent à n’importe quelle théorie de la gravité, dès lors que celle-ci respecte les deux conditions majeures énoncées ci-dessus.

La conséquence principale des travaux de Hawking et Penrose est que l’émergence d’une singularité s’accompagne nécessairement d’un horizon des événements. Penrose ira même jusqu’à proposer l’hypothèse de la censure cosmique, interdisant l’existence de singularités nues (c’est-à-dire sans horizon des événements) ; elle sera réfutée dans les années 1990.

Les singularités gravitationnelles ne sont donc pas des objets physiques tangibles mais uniquement des zones de l’espace-temps dont la géométrie est indéfinie. Elles correspondent aux limites mathématiques de la théorie d’Einstein et peuvent être perçues comme une « pathologie » de la relativité générale. L’émergence de singularités – et donc de divergences, des quantités infinies – au sein des équations d’Einstein montre l’impuissance mathématique de la théorie à décrire certains phénomènes gravitationnels extrêmes. L’existence de singularités signe donc l’incomplétude de la relativité générale.

L’objectif des théories de la gravité quantique actuelles est justement de se débarrasser de ces singularités afin d’obtenir une description cohérente de l’espace-temps, principalement lorsque les phénomènes gravitationnels deviennent si extrêmes qu’ils présentent des effets quantiques. Ainsi, la théorie des supercordes supprime les singularités en les remplaçant par des condensats de supercordes, tandis que la gravitation quantique à boucles les remplace par un rebond quantique. L’absence de singularités au sein d’une théorie de la gravité quantique est un fort indice en faveur de sa cohérence.