Depuis plusieurs années, les pulsars servent d’outils de détection extrêmement puissants pour les physiciens. En effet, grâce à la grande stabilité de leur période de rotation et donc de leur fréquence de pulsation, les pulsars ont permis d’observer plusieurs événements astrophysiques majeurs, que ce soit en terme de physique théorique (1) ou encore de planétologie (2).
L’intérêt des chercheurs s’est notamment porté, ces dernières années, sur l’étude des pulsars au voisinage des objets compacts comme les trous noirs. Ainsi, la découverte du pulsar SGR J174-2900 (3) à proximité du trou noir supermassif SgrA*, situé au centre de la Voie Lactée, a donné la possibilité aux différents télescopes rayons X/rayons gamma/radio d’étudier le comportement du pulsar dans un environnement gravitationnel extrêmement intense.
L’intérêt d’étudier ces systèmes pulsar-trou noir est double (3). Tout d’abord, en étudiant la régularité de la rotation du pulsar et ses potentielles variations, les physiciens peuvent simultanément étudier les propriétés du trou noir. Ensuite, observer le comportement du pulsar plongé dans un important champ gravitationnel permet également de tester directement certains paramètres de la relativité générale.
🔥 Black Friday : -30% de réduction ! 🔥
Utilisez le code : BFRIDAY24
Valable sur tous nos t-shirts (dès 2 articles)
Une invitation à rêver, prête à être portée.
T-shirt de l'Explorateur Éternel
Mais le rôle des pulsars dans de tels systèmes ne s’arrête pas là. En effet, leur étude pourrait également renseigner sur la présence ou non d’un horizon des événements autour de l’objet compact. C’est l’hypothèse que proposent une équipe indienne de physiciens dans une publication parue sur arXiv le 11 novembre 2017 (4).
Les trous noirs et les singularités nues
Les auteurs montrent que la fréquence d’émission d’un pulsar peut être modifiée à proximité d’un objet compact en rotation comme un trou noir de Kerr (trou noir en rotation) ou une singularité nue. La différence entre ces deux objets tient à la présence ou non d’un horizon des événements.
Dans le cadre de la relativité générale, le trou noir de Kerr est une solution aux équations du champ gravitationnel, basée sur la métrique de Kerr. C’est un trou noir décrit par trois paramètres : une masse positive, un moment cinétique (quantité de rotation) non-nul et une charge électrique nulle. En astrophysique, les trous noirs « réalistes » étant réputés en rotation et de charge électrique nulle ou négligeable, le trou noir de Kerr est probablement le « vrai » type de trou noir existant dans la nature.
Une autre solution basée sur la métrique de Kerr existe et diffère du trou noir. Appelée « espace- temps de Kerr rapide », cette solution admet un espace-temps en rotation ultra-rapide, sans horizon des événements, c’est-à-dire une singularité gravitationnelle en rotation dépourvue d’horizon. Une telle singularité est nommée « singularité nue ».
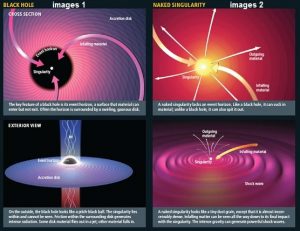
Contrairement à l’idée reçue, en relativité générale, ce n’est pas la singularité gravitationnelle qui définit un trou noir mais bien la présence d’un horizon des événements. Tous les types de trous noirs possèdent nécessairement un horizon des événements ; cette caractéristique commune est l’unique paramètre définissant un trou noir. Dès lors, un trou noir se différencie naturellement d’une singularité nue.
Si la singularité nue est une solution aux équations d’Einstein, sa « réalité » physique reste débattue. Le mathématicien Roger Penrose est le premier à rejeter l’existence des singularités nues en conjecturant le principe de « censure cosmique ». Selon celui-ci, aucune singularité ne peut se former en dehors d’un horizon des événements car dans un tel cas, l’espace-temps présenterait des effets imprévisibles. Puis, en 1986, le cosmologue canadien Werner Israel a démontré que si la rotation d’un trou noir atteint sa fréquence maximale, alors son moment cinétique ralentit, empêchant la formation d’un espace-temps de Kerr rapide.
Mise en évidence d’un horizon des événements grâce aux pulsars
Dans leur étude, les physiciens proposent d’utiliser les pulsars pour discriminer le type d’objet compact autour duquel ils orbitent : trou noir ou singularité nue. Cette discrimination passe par la mise en évidence ou non d’un horizon des événements autour de l’objet. En effet, selon le type d’objet, la dynamique du pulsar ne sera pas la même.
Tout d’abord, le premier paramètre à considérer est la période de rotation du pulsar. Au voisinage d’un objet compact en rotation, la période de rotation du pulsar va être modifiée à cause des effets gravitationnels extrêmement intenses. Cette modification va se traduire par une variation de la fréquence de pulsation mesurée sur Terre.
Autour des trous noirs en rotation, la rotation est si intense que l’espace et la matière sont entraînés dans son mouvement ; ce mouvement d’entraînement porte le nom d’effet Lense-Thirring. La région dans laquelle il se produit est appelée « l’ergosphère ». C’est ce mouvement qui est à l’origine de l’altération de la période de rotation du pulsar.
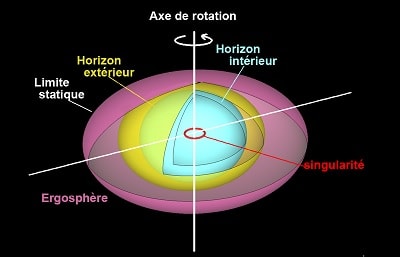
Cependant, la forme de l’ergosphère diffère selon qu’il s’agisse d’un trou noir ou d’une singularité nue. De ce fait, la période de rotation ne sera pas impactée de la même manière. Au voisinage d’un trou noir, la fréquence d’émission du pulsar augmente drastiquement avec sa distance à l’horizon des événements. Plus il se rapproche, plus la fréquence augmente. Ainsi, la détection d’une fréquence de rotation extrêmement élevée – supérieure à 716 Hz (5) – indiquerait la présence d’un horizon.
Dans le cas d’une singularité nue, la fréquence de rotation du pulsar augmente également en fonction de la distance à la singularité, mais de manière beaucoup moins importante. Cela est en partie dû aux effets de marées gravitationnelles qui impactent la structure même du pulsar, avant que sa fréquence ne devienne trop élevée.
Ensuite, le second paramètre à considérer est le devenir du pulsar. Dans le cas d’un trou noir supermassif, les forces de marées ne sont pas suffisamment puissantes pour disloquer le pulsar. En revanche, en s’approchant de l’horizon des événements, sa fréquence de rotation deviendrait telle qu’il finirait par se disloquer sous l’effet de cette rotation extrême. Les auteurs donnent à ce scénario le nom de « phénomène de dislocation par augmentation de la précession du spin » (SPDE).
À l’opposé, dans le cas de la singularité nue, les forces de marées sont suffisamment violentes pour disloquer le pulsar. En effet, aucun horizon ne se trouvant entre la source du champ gravitationnel (la singularité) et sa périphérie, l’intensité gravitationnelle est maximale aux abords de la singularité.
Ces deux scénarios ont des signatures particulières. Pour une dislocation due aux forces de marées gravitationnelles près de la singularité nue, un puissant rayonnement électromagnétique serait émis et capté sur Terre. Alors que pour un SPDE, le pulsar serait suffisamment proche du trou noir pour que l’horizon des événements absorbe la majorité du rayonnement, n’en laissant qu’une infime fraction arriver sur Terre.
Bien évidemment, ce modèle théorique reste assez spéculatif et nécessite des approfondissements. Une des manières d’améliorer le modèle est d’explorer la piste des ondes gravitationnelles émises dans ces scénarios. Si les propriétés des ondes gravitationnelles varient en fonction d’une dislocation par effets de marée ou d’un SPDE, leur étude permettrait également de différencier un trou noir d’une singularité nue.
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]