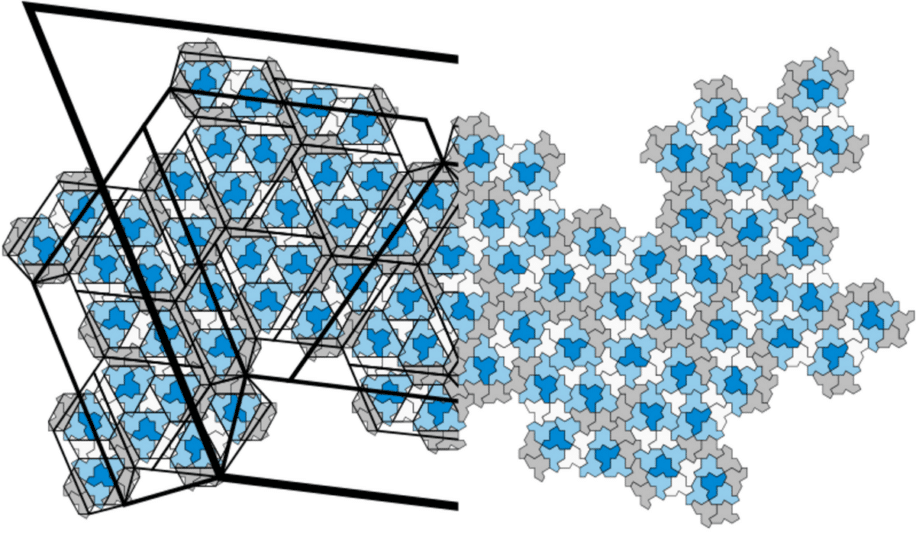
Les pavages « apériodiques » sont de fascinants assemblages géométriques dont les motifs ne se répètent jamais. Jusqu’à il y a peu cependant, les éléments composant ces motifs comportaient au minimum deux formes. Échappant aux mathématiciens pendant plus de dix ans dans le cadre d’un problème de longue date consistant à trouver un monotile apériodique, une forme géométrique à 13 côtés capable à elle seule de former indéfiniment des pavages apériodiques a été découverte. Surnommée polykite « chapeau », la nouvelle forme pourrait bénéficier à un grand nombre de domaines, dont la production de matériaux en mosaïque à la fois solides et esthétiques.
Dans un carrelage, une mosaïque ou un assemblage de tuiles, les pavages périodiques sont les plus couramment observés, probablement pour des raisons de facilité de conception et d’assemblage. Malgré une grande diversité de formes, ce genre de pavage couvre l’espace avec exactement les mêmes motifs se reproduisant indéfiniment. Pourtant, il est assez facile de concevoir un pavage non périodique en utilisant par exemple des tuiles en forme de triangle isocèle et en les assemblant d’une certaine manière. Le pavage apériodique est ainsi davantage utilisé pour des raisons esthétiques dans de nombreuses formes d’art et de décoration.
Parmi les pavages apériodiques les plus célèbres figurent ceux de Penrose, comportant deux formes distinctes pouvant être combinées pour former des motifs qui ne se répètent jamais. En forme de flèche et de cerf-volant par exemple, deux tuiles peuvent d’abord s’emboîter de manière périodique, puis en plaçant la pointe de la flèche au creux du cerf-volant, on obtient un quadrilatère qui peut remplir périodiquement une surface. En revanche, en colorant les sommets des deux tuiles et en les assemblant uniquement par les sommets ayant les mêmes couleurs, on obtient un pavage apériodique. Les pavages de Penrose peuvent également comporter des tuiles en forme de pentagones, de losanges et de pentagrammes entiers ou en portions selon l’assemblage désiré.

Le même principe de couleurs s’applique aux « tuiles de Wang », qui sont composées de carreaux quadricolores divisés selon deux diagonales et qui forment des pavages inévitablement apériodiques. Dans la nature, ces structures apériodiques peuvent être observées dans ce que l’on appelle les « quasicristaux » et dont les lignes de faille se situent exactement entre deux motifs non répétitifs. La plupart des cristaux sont en effet formés par des assemblages d’atomes répétitifs, contrairement aux quasicristaux. Ces derniers ont été observés pour la première fois dans la nature dans un échantillon d’icosahédrite issue d’une météorite tombée dans des montagnes en Russie. Avant cette découverte toutefois, des chercheurs avaient déjà réussi à fabriquer des quasicristaux en laboratoire.
Depuis des décennies, les scientifiques se sont demandé s’il était possible de reproduire la même apériodicité avec une seule forme géométrique. Dans le cadre d’un problème de longue date qui consiste à trouver un monotile apériodique, également connu sous le nom de « einstein » (qui signifie « une pierre » en allemand), de nombreux chercheurs ont longtemps considéré comme impossible l’existence d’une telle forme. Il existerait notamment une infinité de formes de tuiles possibles et l’existence d’une seule solution serait contre-intuitive. En trouvant cette forme unique, capable de paver une surface de manière apériodique, les chercheurs de l’Université de l’Arkansas ont ainsi accompli un véritable exploit.
Une recherche alliant programmation informatique et application pratique
D’après la nouvelle étude, décrite dans une étude parue sur le serveur de préimpression arXiv, la fameuse forme géométrique à 13 côtés a été découverte par le biais de longs calculs informatiques ayant permis d’éliminer toutes possibilités inexploitables. La principale difficulté à identifier une telle forme réside en effet dans le fait de prouver qu’elle peut véritablement s’emboîter de manière apériodique peu importe la façon et le nombre de fois dont on l’assemble à la chaîne. Pour y parvenir, l’équipe de recherche s’est alors à la fois basée sur un algorithme informatique et sur une application empirique (c’est-à-dire un assemblage manuel).
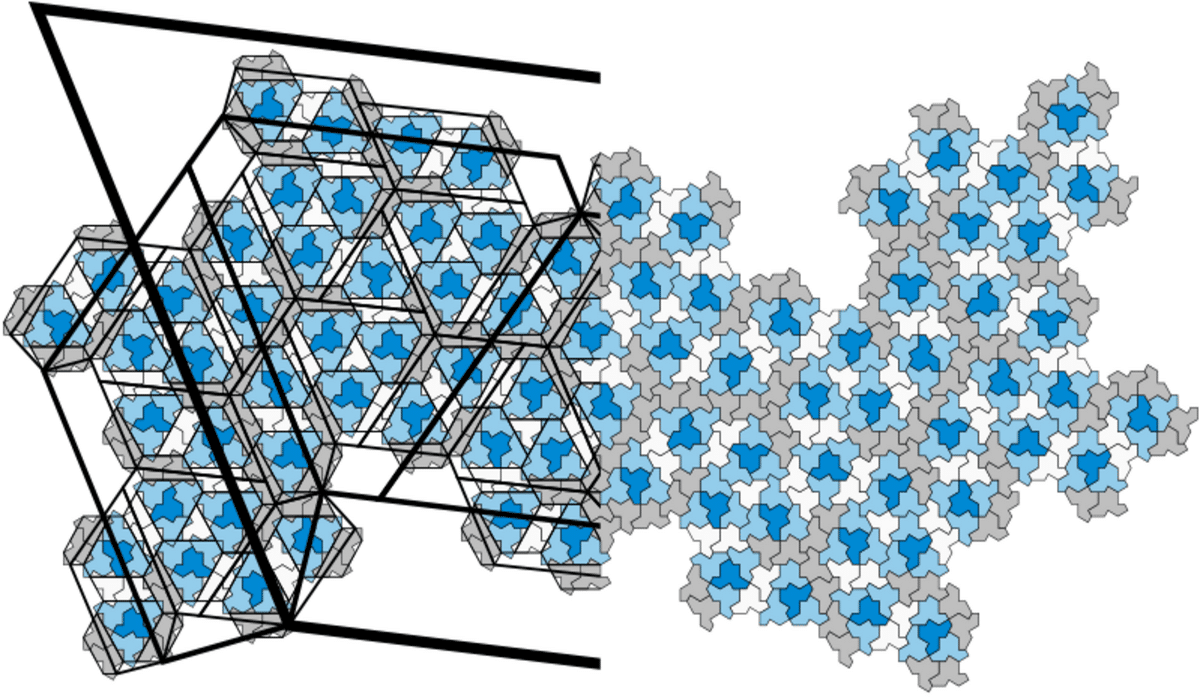
La découverte de cette nouvelle forme pourrait découler sur un grand nombre d’applications potentielles, non seulement dans la science des matériaux, mais aussi dans le domaine des arts décoratifs. Les pavages reposant sur cette forme permettraient notamment de développer de nouveaux matériaux d’une grande stabilité.