Loto : quelles sont réellement les chances de gagner ? Est-il possible de contourner le système ?

Qui n’a jamais un jour imaginé gagner au loto ? Que ce soit le loto français ou le système EuroMillions, les gains pour le jackpot sont souvent considérables. De telles sommes sont certes extrêmement attirantes, mais encore faut-il parvenir à les gagner. Et à ce sujet, les mathématiques nous rappellent que la victoire est loin, très loin d’être aisée.

Malgré les quelques personnes affirmant qu’il est possible de gagner presque à tous les coups ou encore qu’il est possible de prédire infailliblement la combinaison gagnante du loto, faisons d’ores et déjà tomber ce mythe : c’est totalement faux. Seul le hasard gouverne le tirage du loto. Il y a en effet équiprobabilité entre les numéros, c’est-à-dire que chaque numéro a la même probabilité d’être tiré que les autres. Cette implacabilité des lois de la probabilité rend donc toute tentative de prédiction superflue.

Le loto : un système entièrement soumis aux probabilités

Depuis le 6 octobre 2008, le système du loto français est le suivant : un joueur doit obtenir 5 numéros parmi 49 ainsi qu’un « numéro chance » parmi 10. Il est possible de calculer le nombre de grilles différentes possibles en calculant les coefficients binomiaux C⁵₄₉ et C¹₁₀. La formule d’un coefficient binomial Cⁿ_m est la suivante :

Cⁿ_m = n!/n!(m-n)! Cette formule permet de connaître le nombre de combinaisons de n éléments compris dans un ensemble de m éléments. Le signe « ! » désigne la factorielle d’un nombre, c’est-à-dire le produit de tous les entiers compris entre 1 et ce nombre. Par exemple :

5! = 5×4×3×2×1 = 120 Prenons l’exemple d’une classe de 8 élèves organisant un voyage scolaire, mais il n’y a de place que pour 3 élèves. Chacun a les mêmes chances que les autres d’être sélectionné. Il existe ainsi C³₈ combinaisons possibles de trois élèves, soit :

C³₈ = (8×7×6)/(3×2) = 56 combinaisons L’équiprobabilité des combinaisons entraîne donc l’impossibilité de contourner la nature probabiliste des tirages. Cependant, il est possible d’augmenter ses chances en multipliant le nombre de combinaisons jouées ; là également, il s’agit d’une pure question de probabilités. Ainsi, jouer plusieurs grilles à la fois, seul ou avec des « complices », permet de couvrir un plus grand nombre de combinaisons. Par exemple, pour un loto possédant 500’000 combinaisons possibles, jouer 25’000 grilles permet de couvrir 5% de toutes les combinaisons.

Il est possible de pousser le stratagème encore plus loin en utilisant la théorie des jeux et plus particulièrement en atteignant l’équilibre de Nash. L’équilibre de Nash est une situation dans laquelle chaque joueur prévoit correctement le choix des autres, maximisant ainsi ses chances de gain. Lorsqu’un groupe de joueur agit en parfaite coordination et que chaque joueur sélectionne une combinaison par rapport aux combinaisons des autres joueurs, alors l’équilibre de Nash peut être atteint et les chances de gains augmentées de 10 à 25%.

Loto français et EuroMillions : quelles sont les chances de gagner le jackpot ?

Maintenant que nous savons comment calculer l’ensemble des combinaisons possibles pour un système à m éléments, il est intéressant de calculer les chances de gagner au loto français et à l’EuroMillions. Appliqué au loto français, le nombre de grilles possibles est donné par :

C⁵₄₉×C¹₁₀ = ((49×48×47×46×45)/(1×2×3×4×5))×(1/10) = 19’068’840 grilles différentes possibles Avec une seule grille, la chance de trouver les 5 numéros + le numéro chance gagnants (rang 1) est donc de 1 sur 19’068’840, soit une probabilité d’environ 0,00000524 %. Au rang 2, c’est-à-dire 5 numéros gagnants sans le numéro chance, la chance passe à 1 sur 2’118’760, soit une probabilité d’environ 0,000047 %. Plus le rang augmente, plus les probabilités de victoire augmentent, mais plus les gains baissent considérablement également.

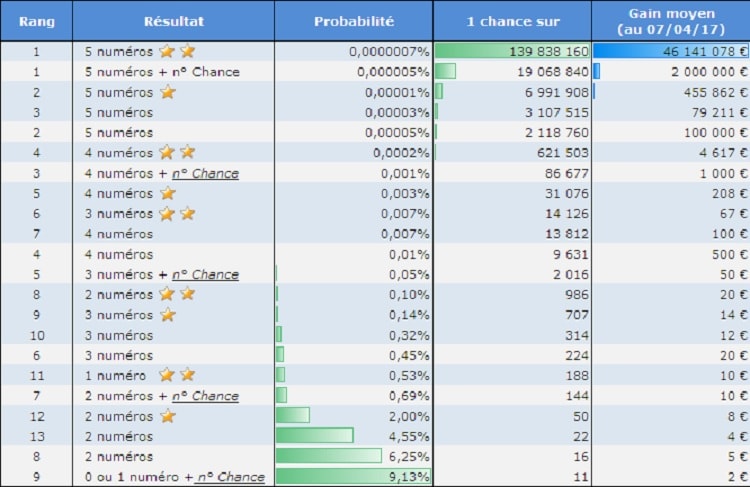
Il est possible de mettre en lumière la probabilité extrêmement faible de gagner le rang 1 avec cette comparaison : en France, selon l’INSEE, le quotient de mortalité des hommes de 52 ans est de 594 pour 100’000. Lorsqu’un homme de 52 ans achète un billet de loto, la probabilité de gagner le rang 1 est identique à celle de décéder dans les 4 minutes et 38 secondes suivantes. En effet, cette probabilité est donnée par :

P_(décès) = (594×4.64)/(100000×365×24×60) = 1/19’068’840 Concernant l’EuroMillions, le système utilisé réduit encore plus les chances de gagner. Le jeu consiste à choisir 5 numéros entre 1 et 50 ainsi que deux étoiles numérotées de 1 à 12. La probabilité de sélectionner les 5 bons numéros est de 0,000047 %, et celle de sélectionner les 2 bonnes étoiles est de 1.52 %. Le nombre de combinaisons possibles est donné par :

C⁵₅₀×C²₁₂ = 139’838’160 combinaisons possibles C’est-à-dire 1 chance sur 139’838’160 de trouver la bonne combinaison, soit une probabilité de 0.00000072 %.

Stefan Mandel, ou l’homme qui a tenté de défier le système du loto

N’existe-t-il alors aucune technique permettant de remporter le jackpot à coup sûr ? Le mathématicien et économiste roumain Stefan Mandel n’en serait pas si sûr. En 1992, Mandel décide de battre le système du loto à son propre jeu en jouant tout simplement la totalité des combinaisons possibles. Pour cela, il se fixe deux conditions préalables : la somme à gagner ne doit pas être inférieure à la somme investie, et toutes les combinaisons possibles doivent être sélectionnées en un temps limité, en évitant les doublons.

Le mathématicien jette son dévolu sur une loterie organisée par l’État de la Virginie, dont le gain s’élève à 28 millions de dollars. Pour cette loterie, il existe 7’059’052 combinaisons différentes, et la mise pour chaque grille est de 1 dollar. Aidé de plusieurs de ses amis, Mandel prend peur lorsqu’à la fin du temps imparti, son équipe n’a réussi à jouer que 5 millions de combinaisons, soit environ 70% des grilles possibles, et donc 30% de risque de perdre 5 millions de dollars. Heureusement pour lui, la chance est de son côté et il empoche la jackpot.

Toutefois, il n’aura jamais l’occasion d’en profiter. Le gouvernement australien s’étant aperçu de la stratégie de Mandel, et ne pouvant le sanctionner pénalement car il ne s’agissait pas d’une fraude, a rapidement créé tout un ensemble de taxes qui ont fini par ruiner le mathématicien, l’argent retournant inexorablement au gouvernement sous forme d’impôts. Cette histoire est une piqûre de rappel pour tous les joueurs : au loto, seul le hasard est roi.