Lorsque l’on plonge un glaçon dans l’eau, celui-ci fond progressivement, mais sans jamais adopter de formes atypiques, dotées d’arêtes et de pointes acérées. Au contraire, les arêtes du cube initial s’estompent peu à peu. Des dizaines d’années de recherche auront été nécessaires pour parvenir à comprendre pleinement les équations qui permettent de modéliser la fusion de la glace dans l’eau. Aujourd’hui, une équipe de mathématiciens prouvent que les résultats du calcul sont bien conformes à ce que l’on observe dans la réalité.
La question de savoir comment la glace fond dans l’eau est un exemple du « problème de Stefan », du nom du physicien Josef Stefan, qui l’a énoncé en 1889. C’est un problème dit de « frontière libre », où il s’agit de comprendre comment un processus, tel que la diffusion de chaleur, modifie la frontière qui sépare deux phases de la matière (ici, la frontière entre la glace et l’eau). La modélisation mathématique de ces frontières est particulièrement complexe ; cela nécessite de résoudre les équations de chaleur dans les deux régions, sous réserve de conditions limites et initiales données.
Dans une étude publiée au mois de mars sur arXiv, une équipe de mathématiciens suisses explique comment elle s’est inspirée de recherches antérieures sur les films de savon pour prouver qu’au cours de la transition de phase entre la glace et l’eau, des cuspides ou des arêtes — des points aigus que les chercheurs nomment « singularités » — se forment rarement, et que même lorsque cela arrive, elles disparaissent immédiatement.
Un petit écart, source de singularités
Lorsque l’on plonge un glaçon dans l’eau, celle-ci existe alors dans deux phases différentes : solide et liquide. Une frontière existe là où les deux phases se rencontrent, mais à mesure que la chaleur de l’eau est transférée à la glace, cette dernière fond et la frontière se déplace. Puis, la glace (tout comme la frontière) finit par disparaître. L’observation du phénomène suggère que la frontière de fusion reste toujours lisse. Mais serait-il possible qu’une zone pointue émerge soudainement lors de la fonte ? Jusqu’à présent, les modèles mathématiques n’avaient en tout cas jamais réussi à prouver que c’était inenvisageable.
Pour résoudre le problème de Stefan, les chercheurs ont dû prouver que les singularités qui surgissent dans les équations sont contrôlées, en d’autres termes, qu’elles sont très rares et qu’elles ne durent pas longtemps. Pour ce faire, ils avaient besoin d’une compréhension globale de tous les différents types de singularités qui pourraient éventuellement se former.
Il y a quelques années, grâce aux travaux réalisés sur la modélisation des films de savon qu’il a adaptés au problème de Stefan, le mathématicien Luis Caffarelli avait progressé dans la compréhension de la façon dont les singularités se développent à mesure que la glace fond. Il a notamment conçu un moyen d’estimer leur nombre : il a découvert qu’à mesure que l’on s’éloigne d’une singularité, la température augmente de manière claire. Plus précisément, il a déterminé que la température de l’eau autour d’une singularité suivait un modèle paraboloïde — une parabole en 3D, car l’espace est tridimensionnel et il est possible de s’éloigner de la singularité dans trois directions différentes.
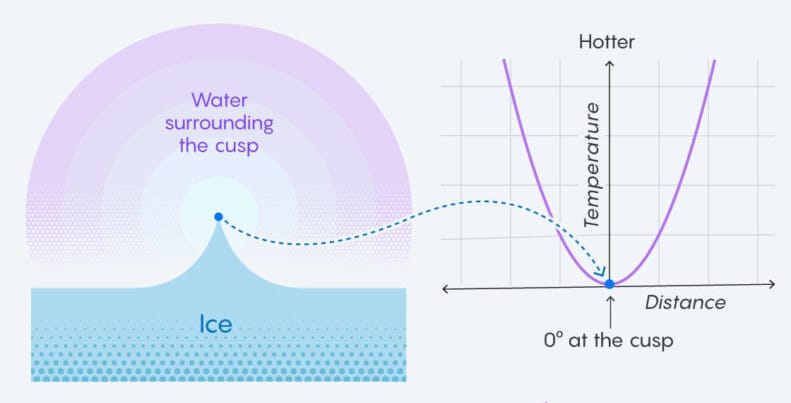
Mais Caffarelli a également reconnu que la température ne suivait pas exactement ce schéma : il existait un petit écart entre un paraboloïde parfait et l’apparence réelle de la courbe de température de l’eau. Alessio Figalli, Xavier Ros-Oton et Joaquim Serra, de l’École polytechnique fédérale de Zurich, ont entrepris d’examiner cette déviation d’un peu plus près. Ils ont alors découvert que cet écart par rapport au modèle avait ses propres types de motifs, qui donnaient naissance à différents types de singularités.
Des motifs trop éphémères pour être observés
Les chercheurs sont parvenus à démontrer que tous ces nouveaux types de singularités disparaissaient rapidement — comme dans la nature — à l’exception de deux d’entre eux, particulièrement énigmatiques. Restait donc à prouver ces deux types de singularités étaient tout aussi éphémères, excluant définitivement la possibilité qu’une forme pointue puisse perdurer lorsqu’un glaçon fond. Là encore, ils ont pu s’appuyer sur les recherches effectuées auparavant sur les films de savon.
Le premier type de singularité avait déjà été décrit en 2000, par le mathématicien Frederick Almgren. Alors qu’il était admis que les films de savon sont toujours lisses en trois dimensions, Almgren a prouvé qu’en quatre dimensions, un nouveau type de singularité « ramifiée » peut apparaître, rendant les films de savon « tranchants ». Ces singularités sont profondément abstraites et impossibles à visualiser ; pourtant, Figalli, Ros-Oton et Serra ont réalisé que des singularités très similaires se forment le long de la frontière de fusion entre la glace et l’eau.
Ils ont utilisé le travail d’Almgren pour montrer que la glace autour de l’une de ces singularités ramifiées doit avoir un motif conique ; or, un motif conique ne peut avoir une singularité nette qu’en un seul point. De ce fait, les chercheurs ont montré que ces singularités sont isolées dans l’espace et dans le temps : dès qu’elles se forment, elles disparaissent.
Le second type de singularité était encore plus mystérieux : imaginez une fine couche de glace immergée dans l’eau ; elle rétrécira progressivement, jusqu’à disparaître soudainement d’un seul coup. Juste avant cet instant précis, elle formera une singularité en forme de feuille, une frontière bidimensionnelle aussi tranchante qu’un rasoir. L’équipe a néanmoins prouvé par le calcul qu’une telle singularité était nécessairement éphémère elle aussi. Après avoir levé le doute sur ces deux singularités spécifiques, les chercheurs ont pu affirmer de manière générale que toutes les singularités du problème de Stefan sont rares. « Si vous choisissez un moment au hasard, la probabilité d’observer un point singulier est nulle », résume Ros-Oton pour Quanta Magazine.

