Au cours du deuxième Congrès international des mathématiciens tenu à Paris au mois d’août 1900, le mathématicien allemand David Hilbert énonce une liste de 23 problèmes mathématiques dont la résolution constituerait une avancée capitale dans le développement de la discipline. Au début des années 2000, l’Institut de mathématiques Clay sélectionne 7 problèmes particuliers et propose une importante rémunération pour la résolution de chacun d’eux.
Fondé en 1998 par l’homme d’affaires Landon Clay, l’Institut mathématique du même nom s’est donné pour mission de promouvoir les mathématiques à travers le monde et d’encourager la recherche dans ce domaine. Dans ce but, l’Institut a instauré un système de prix et de primes afin de récompenser les mathématiciens ayant effectué d’importantes avancées et contributions dans toutes les branches des mathématiques. Ces récompenses comportent, entre autre, les Problèmes du prix du millénaire. Ces derniers constituent un ensemble de 7 problèmes mathématiques irrésolus choisis parmi les hypothèses et conjectures mathématiques actuelles. La résolution de chaque problème entraînant l’attribution d’un prix d’un million de dollars américains décerné par l’Institut Clay.
L’exercice demandé aux mathématiciens est la démonstration rigoureuse d’une hypothèse ou conjecture, ou alors la détermination précise de solutions à certaines équations. Une fois publiée, la solution doit faire consensus au sein de la communauté scientifique mathématique pendant une durée de deux ans. Si ces deux conditions sont remplies, le prix est décerné à la personne ou au groupe de personnes à l’origine de la publication. La résolution de ces 7 problèmes serait considérée comme un approfondissement majeur des mathématiques fondamentales.
Bien que tous les scientifiques s’accordent sur la nécessité de résoudre ces problèmes, l’attribution d’un prix ne fait pas l’unanimité. L’importante couverture médiatique des problèmes du prix du millénaire a cependant été l’occasion de relancer l’intérêt du public et des étudiants pour les mathématiques, discipline de plus en plus délaissée et dont la réforme en France a été récemment confiée au député Cédric Villani ; contenant 21 nouvelles mesures, cette réforme insiste particulièrement sur l’utilisation de site et forum de mathématiques dans l’apprentissage de cette discipline mal-aimée.
1. L’hypothèse de Riemann
En novembre 1859, le mathématicien allemand Bernhard Riemann publie un article intitulé « Sur le nombre de nombres premiers inférieurs à une taille donnée » dans les Rapports mensuels de l’Académie de Berlin et dans lequel il mentionne pour la première fois une conjecture concernant la fonction zêta. La fonction zêta de Riemann est une fonction analytique complexe dont la position des zéros complexes conditionne la répartition des nombres premiers.
Riemann conjecture que les zéros non-triviaux de la fonction zêta ont tous pour partie réelle 1/2 (cette conjecture deviendra l’hypothèse de Riemann). Il propose alors que tous ces zéros doivent être distribués dans la bande critique 0 < Re(s) < 1 et qu’ils pourraient même être tous distribués sur la ligne critique Re(s) = 1/2. Il démontrera que c’est le cas pour les premiers zéros de la fonction zêta puis laissera cette hypothèse de côté pour poursuivre d’autres objectifs. Malgré quelques avancées, l’hypothèse de Riemann ne possède toujours pas de démonstration.
2. La conjecture de Poincaré

Le mathématicien français Henri Poincaré énonce la conjecture suivante en 1904 : « Soit une variété compacte V simplement connexe, à 3 dimensions, sans bord. Alors V est homéomorphe à une hypersphère de dimension 3 ». En termes très simples, Poincaré propose qu’un objet topologique 3D aux propriétés identiques à celles d’une 3-sphère (sphère tridimensionnelle) est homéomorphe à une 3-sphère (c’est-à-dire que les deux objets sont les mêmes mais « vus différemment ».
La démonstration de cette conjecture est importante car elle clôt la classification des variétés en trois dimensions. Elle a été apportée par le mathématicien russe Grigori Iakovlevitch Perelman en 2003 qui a, par suite, refusé l’attribution de la médaille Fields ainsi que celle du prix d’un million d’euros de l’Institut Clay. Actuellement, la conjecture de Poincaré est le seul problème du millénaire a avoir été résolu.
3. La conjecture de Hodge
Entre 1930 et 1940, le mathématicien écossais William Vallance Douglas Hodge énonce une importante conjecture concernant la géométrie algébrique : tout calcul de la cohomologie d’une variété algébrique projective complexe à partir de ses sous-variétés est possible. Cette conjecture étend les travaux du mathématicien Georges de Rham sur la théorie cohomologique. La démonstration du lien topologique entre une variété algébrique est sa géométrie donnée par les équations définissant ses sous-variétés, constituerait un approfondissement important de l’étude des variétés différentielles.
4. Le problème P = NP
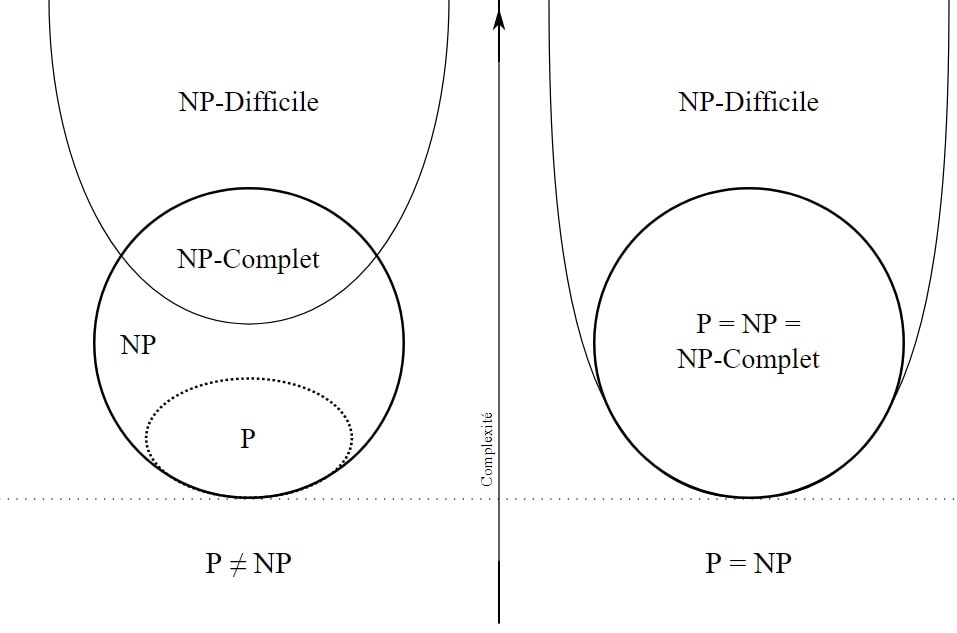
Le problème P = NP est une conjecture capitale dans le domaine des mathématiques et de l’informatique théorique. Considéré par les théoriciens comme le problème le plus important, sa démonstration aurait de très profondes implications. Cette conjecture peut être résumée comme le fait de savoir si la recherche d’une solution à un problème peut être aussi rapide que de vérifier si une réponse donnée constitue effectivement une réponse valable à ce problème.
Plus techniquement, le problème P = NP met en jeu deux classes de complexité (la complexité désigne la quantité de ressources nécessaire pour qu’un algorithme résolve un problème en un temps donné). La classe P (pour polynomiale) désigne un problème de décision pouvant être décidé par une machine de Turing déterministe en un temps polynomial ; ce sont donc des problèmes pouvant être résolus relativement rapidement.
La classe NP (pour non-déterministe polynomiale) désigne un problème de décision pouvant être décidé par une machine de Turing non-déterministe en un temps polynomial ; cela permet de vérifier rapidement que des solutions candidates sont bien des solutions.
La démonstration P = NP offrirait une résolution pour tous les problèmes NP-complets (biologie, commerce, transports, etc) en temps polynomial, c’est-à-dire prouverait qu’un algorithme est capable de résoudre rapidement un problème de décision. Un tel résultat permettrait théoriquement de solutionner l’ensemble de tous les autres problèmes du millénaire. Au contraire, la démonstration P ≠ NP prouverait qu’il est impossible de résoudre les problèmes NP-complets en temps polynomial et donc que de nombreux problèmes resteront insolubles.
5. La conjecture de Birch et Swinnerton-Dyer
En 1960, les mathématiciens britanniques Bryan Birch et Peter Swinnerton-Dyer utilisent un ordinateur particulier de l’université de Cambridge, l’Electronic Delay Storage Automatic Calculator (ESDAC), afin de calculer le nombre de points modulo p « Np » pour plusieurs nombres premiers p présents sur des courbes elliptiques de rang connu. Les résultats obtenus leur permettent d’émettre une conjecture sur la dynamique de la fonction L (prolongement analytique complexe de la série de Dirichlet) d’une courbe elliptique en s = 1 : il y a toujours un zéro d’ordre r en ce point.
Cette conjecture est réputée être l’un des problèmes mathématiques les plus complexes et constitue une proposition vraiment innovante, car c’est la première qui étend le cas d’annulation de la fonction L en s = 1 aux courbes elliptiques, alors qu’auparavant il n’était circonscrit qu’aux courbes avec multiplication complexe.
6. Les équations de Navier-Stokes
Nommées en l’honneur de l’ingénieur français Henri Navier et du physicien britannique Georges Gabriel Stokes, les équations de Navier-Stokes sont des équations aux dérivées partielles non-linéaires décrivant la dynamique des fluides newtoniens. Bien qu’il existe des solutions approchées permettant de modéliser des phénomènes comme les courants océaniques et les mouvements atmosphériques, la résolution exacte de ces équations est particulièrement complexe et il n’existe actuellement aucune solution générale ni aucune démonstration mathématique rigoureuse de celles-ci.
L’objectif est ici de confirmer ou infirmer la proposition suivante : dans un problème temporel en dimension 3 d’espace pour lequel on spécifie une condition initiale, il existe des champs de vitesse et de pression scalaire réguliers qui sont solutions des équations de Navier-Stokes. Cette proposition est directement reliée à la recherche de solutions modélisant la dynamique d’un fluide incompressible dans l’approximation des milieux continus. La résolution mathématique de ces équations offrirait d’importantes avancées dans la modélisation des turbulences et des écoulements.
7. Les équations de Yang-Mills
Ces équations constituent le cadre mathématique des théories de Yang-Mills. Une théorie de Yang-Mills, nommée à partir de ses auteurs, les physiciens Chen Ning Yang et Robert Mills, est une théorie de jauge (théorie des champs basée sur une symétrie locale) développée initialement en 1950 pour décrire la cohésion nucléon-nucléon au sein du noyau atomique. Par la suite, combinée à la théorie quantique des champs, elle fut généralisée à l’ensemble des interactions fondamentales et constitue aujourd’hui la base du Modèle Standard.
Bien que son cadre géométrique soit bien compris, les équations de Yang-Mills sont des équations non-linéaires dont la résolution s’avère très ardue. En outre, deux démonstrations mathématiques doivent encore être apportées. La première concerne l’existence d’une théorie quantique des champs intégrée à une théorie de Yang-Mills, autre qu’une théorie libre (déjà démontrée dans le cadre de la théorie constructive des champs). La seconde concerne l’existence d’un « gap de masse », c’est-à-dire la différence d’énergie entre l’état fondamental et l’état suivant de plus basse énergie conduisant à l’apparition de « glueballs » (balles de gluons) dont les gluons ne peuvent être observés que sous cette forme.
De nombreux mathématiciens travaillent actuellement sur la résolution des problèmes du millénaire, notamment plusieurs mathématiciens français. L’Institut Henri Poincaré est, à ce titre, un acteur majoritaire de la recherche et de la promotion des mathématiques en France. Peut-être faites-vous ou ferez-vous partie des futurs grands gagnants ? Henri Poincaré disait que les mathématiques étaient le plus court chemin vers la poésie et que n’importe qui peut devenir poète. Bacheliers cherchant désespérément des cours de maths niveau Terminale, collégiens ambitieux, chercheurs accomplis ou tout simplement autodidactes rêveurs, le million de dollars est à portée de main.

