Grâce à l’intelligence artificielle développée par Google DeepMind, des chercheurs de l’Université de Sydney rapportent avoir résolu des problèmes de mathématiques pures, particulièrement complexes, du domaine de la théorie des nœuds et de la théorie des représentations. C’est la première fois que l’apprentissage automatique (ou machine learning) est mis à profit pour prouver de nouveaux théorèmes, mettant en évidence des modèles mathématiques inédits.
« Les problèmes mathématiques sont largement considérés comme certains des problèmes les plus difficiles sur le plan intellectuel », a déclaré Geordie Williamson, mathématicien à l’Université de Sydney en Australie et co-auteur de l’étude. La pratique des mathématiques consiste à découvrir des modèles et à les utiliser pour formuler et prouver des conjectures, qui aboutissent à des théorèmes. Depuis les années 1960, les mathématiciens s’appuient sur des ordinateurs pour mener leurs recherches. L’apprentissage automatique est d’ailleurs largement exploité en mathématiques expérimentales, pour générer et analyser des ensembles de données complexes.
Williamson a appliqué la puissance des processus d’IA de DeepMind pour explorer des conjectures dans son domaine de spécialité : la théorie des représentations — une branche qui étudie les structures algébriques abstraites en représentant leurs éléments comme des transformations linéaires d’espaces vectoriels, et qui étudie les modules sur ces structures algébriques abstraites. C’est la première fois que le machine learning contribue à formuler des conjectures et à suggérer des angles d’attaque possibles pour prouver des théorèmes.
Des découvertes qui profitent à plusieurs disciplines
Le professeur Geordie Williamson est directeur de l’Institut de recherche mathématique de l’Université de Sydney et l’un des plus grands mathématiciens du monde. En 2018, il a été élu le plus jeune membre vivant de la Royal Society de Londres, l’association scientifique la plus ancienne et l’une des plus prestigieuses au monde. Il s’intéresse tout particulièrement à la théorie des représentations, une branche des mathématiques qui permet de réduire des problèmes d’algèbre abstraite à des problèmes d’algèbre linéaire — un domaine plus « accessible » et mieux maîtrisé.
La théorie des représentations est très importante, car elle est omniprésente dans tous les domaines des mathématiques et a conduit à de nombreuses généralisations. Néanmoins, l’identification de nouveaux modèles est une tâche particulièrement ardue. « Travailler pour prouver ou réfuter des conjectures de longue date dans mon domaine implique la prise en compte, parfois, d’un espace infini et d’ensembles d’équations extrêmement complexes à travers plusieurs dimensions », explique le professeur Williamson. C’est pourquoi le spécialiste a entrepris d’utiliser l’IA de DeepMind pour l’assister dans ses recherches.
Le mathématicien avait en particulier pour objectif de prouver une vieille conjecture sur les polynômes de Kazhdan-Lusztig, qui demeure non résolue depuis 40 ans ; cette conjecture concerne la symétrie profonde dans l’algèbre de dimension supérieure.
Ses collaborateurs, le professeur Marc Lackeby et le professeur András Juhász de l’Université d’Oxford, ont poussé le processus un peu plus loin : c’est ainsi qu’ils ont découvert une nouvelle connexion entre les invariants algébriques et géométriques des nœuds, menant à un théorème complètement nouveau en mathématiques. Dans la théorie des nœuds, les invariants sont utilisés pour résoudre le problème de la distinction des nœuds entre eux ; ils aident également les mathématiciens à comprendre les propriétés des nœuds et leur lien avec d’autres branches des mathématiques. La théorie des nœuds a également de nombreuses applications dans d’autres disciplines scientifiques ; elle aide par exemple à comprendre les brins d’ADN, la dynamique des fluides ou encore l’interaction des forces dans la couronne solaire. Les découvertes réalisées en mathématiques grâce à l’IA peuvent donc servir à de nombreux autres domaines de recherche.
Trouver des connexions que l’esprit humain ne repère pas toujours
« Les mathématiciens purs travaillent en formulant des conjectures et en les prouvant, ce qui aboutit à des théorèmes », explique le professeur Juhász. Encore faut-il réussir à établir ces conjectures, qui sont la plupart du temps établies sur simple intuition des mathématiciens ! Ceci est particulièrement complexe dans des domaines où une grande quantité de données est disponible, ou lorsque les objets sont trop grands pour être étudiés avec des méthodes classiques.
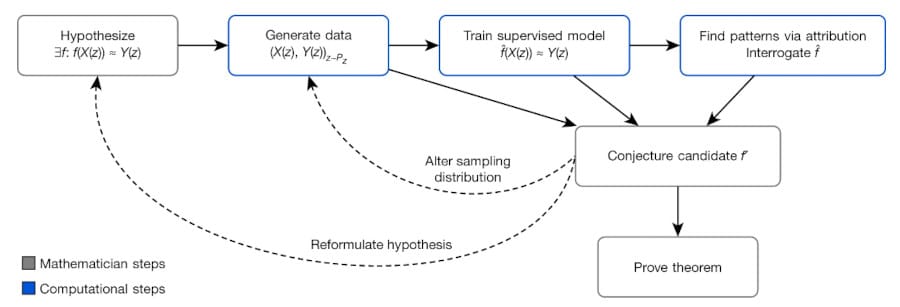
C’est là que le machine learning peut véritablement faire la différence : ces systèmes d’IA peuvent rechercher des modèles et des scénarios inédits, simplement en appliquant les principes tirés de leurs données d’entraînement à de nouvelles situations. « Lorsqu’il est guidé par l’intuition mathématique, l’apprentissage automatique fournit un cadre puissant qui peut découvrir des conjectures intéressantes et prouvables », confirme Juhász.
L’équipe a donc prouvé que l’apprentissage automatique peut être utilisé en mathématiques pures, pour découvrir des modèles et des relations potentielles entre les objets, des connexions nouvelles et inattendues entre différents domaines des mathématiques, qui peuvent être exploitées pour guider l’intuition vers de nouvelles conjectures. « Je pense que le travail que nous avons réalisé à Oxford et à Sydney en collaboration avec DeepMind démontre que l’apprentissage automatique peut être un outil véritablement utile dans la recherche mathématique », a déclaré le professeur Lackeby. « L’intuition peut nous mener loin, mais l’IA peut nous aider à trouver des connexions que l’esprit humain ne repère pas toujours facilement », a ajouté Williamson.
Les auteurs espèrent que leur travail pourra servir de modèle pour approfondir la collaboration entre les domaines des mathématiques et de l’intelligence artificielle afin d’obtenir des résultats surprenants, en tirant parti des forces respectives de chaque discipline. « Mon espoir est que l’IA puisse nous fournir un autre axe d’intelligence avec lequel travailler, et que ce nouvel axe approfondisse notre compréhension du monde mathématique », conclut Williamson.


