Formulée en 1859 par le mathématicien allemand Bernhard Riemann, l’hypothèse de Riemann est l’un des problèmes mathématiques non-résolus les plus importants du 21ème siècle. Elle est l’un des sept problèmes du millénaire posés par l’Institut de mathématiques de Clay. Le mathématicien anglais Michael Atiyah, mondialement reconnu dans son domaine, a récemment proposé une solution à l’hypothèse de Riemann. Solution qui ne semble toutefois pas emporter toute l’adhésion de la communauté scientifique.
Michel Atiyah est un mathématicien reconnu pour ses nombreuses contributions dans les domaines de la géométrie, de la topologie et de la physique théorique. Pour ses travaux, il a reçu deux des récompenses les plus prestigieuses décernées aux mathématiciens : la médaille Fields en 1966 et le Prix Abel en 2004.
Sur le même sujet :
Mathématiques : 7 problèmes fondamentaux pour le prix du millénaire
Atiyah a annoncé avoir trouvé une solution à l’hypothèse de Riemann, une conjecture énoncée il y a 160 ans et toujours irrésolue. Intégrée aux sept problèmes du millénaire, sa résolution, comme pour les six autres problèmes de la liste, est récompensée d’un prix d’un million de dollars. Mais avant d’en arriver là, le travail du mathématicien devra être évalué par les pairs puis être publié dans une revue scientifique avant de pouvoir réclamer sa récompense à l’Institut Clay.
Qu’est-ce que l’hypothèse de Riemann ?
À la fin des années 1850, Riemann travaille sur la distribution des nombres premiers, c’est-à-dire des nombres divisibles uniquement par 1 ou par eux-mêmes. Le mathématicien allemand suggère que cette distribution n’est pas aléatoire, mais suit un schéma décrit par une formule particulière : la fonction zêta de Riemann, possédant une partie réelle et une partie imaginaire. Plus précisément, la répartition des nombres premiers serait liée aux zéros de cette fonction.
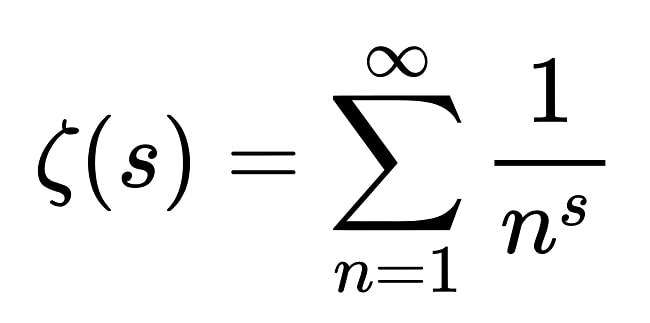
Pour que cette répartition soit en accord avec la formule, les zéros non-triviaux de la fonction zêta de Riemann doivent avoir pour partie réelle 1/2. Riemann lui-même a prouvé cette propriété pour les nombres premiers du début de la liste, et dans les années suivantes, les algorithmes informatiques ont vérifié 10’000’000’000’000 de zéros, tous satisfaisant l’hypothèse de Riemann. Toutefois, cette dernière doit être formellement démontrée jusqu’à l’infini.
Démontrer l’hypothèse de Riemann n’a pas qu’une incidence théorique, mais pourrait également avoir des applications pratiques dans des processus utilisant la prédiction des nombres premiers. C’est particulièrement le cas de certains protocoles de cryptographie algébrique avancés dans lesquels des séquences de nombres premiers doivent être générés et manipulés.
La solution d’Atiyah : de l’incompréhension au scepticisme
Lors d’une conférence de 45 min donnée au Heidelberg Laureate Forum (Allemagne), Sir Michel Atiyah, mathématicien émérite de l’université d’Édimbourg (Écosse), a présenté une solution à la conjecture de Riemann qui a, pour le moins, suscité la surprise et l’étonnement de ses pairs.
En effet, ce qu’Atiyah a décrit comme une « preuve simple », repose sur une notion de physique à première vue sans rapport avec le problème mathématique concerné : la constante de structure fine, notée α. C’est un des 29 paramètres libres du Modèle Standard, et, dans la théorie de l’électrodynamique quantique (théorie quantique de l’électromagnétisme), elle décrit la force de l’interaction entre les électrons et les protons. Constante sans dimension, sa valeur est uniquement mesurée, le mécanisme mathématique sous-tendant cette valeur étant toujours inconnu.
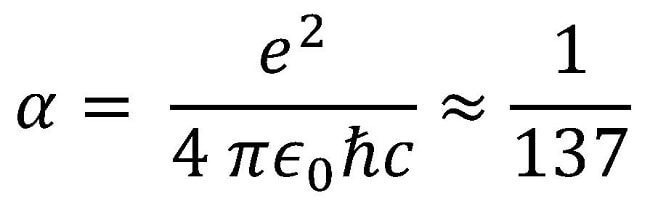
Dans le papier rendu public par Atiyah, celui-ci présente une méthode visant à dériver mathématiquement la valeur de la constante de structure fine à partir de la fonction de Todd, notée T, une fonction mathématique dont il est lui-même l’auteur et sur laquelle il n’a révélé que très peu d’informations. Dans son article, le mathématicien montre simplement que que sur la ligne critique de la fonction zêta de Riemann, celle ayant pour partie réelle 1/2, la fonction de Todd a une limite en ж à partir de laquelle on retrouve la constante de structure fine :
Selon Jørgen Veisdal, mathématicien et économiste à l’université des Sciences et Techniques de Norvège ayant travaillé sur la conjecture de Riemann, « il est très peu probable que la proposition d’Atiyah soit une solution de l’hypothèse de Riemann telle que nous la connaissons. C’est simplement trop vague et trop peu spécifique ».
Plusieurs des collègues d’Aityah n’ont pas souhaité s’exprimer publiquement, pour ne pas être en mauvais termes avec le mathématicien, mais l’opinion générale tend tout de même à considérer que les travaux de ce dernier ne représentent pas une solution viable à l’hypothèse de Riemann. Pour John Baez, physicien mathématicien à l’université de Californie, « cette preuve ne fait qu’empiler des déclarations grandiloquentes sans réelle connexion les unes avec les autres, ni véritable substance de fond ».
Tandis que, pour sa part, Atiyah semble imperturbable devant ces critiques. Il écrivait dans un e-mail quelques jours avant sa présentation « je me jette aux lions, j’espère en sortir indemne ». Dans une interview, il expliquait que, en dépit des critiques, ses travaux posent une base concrète solutionnant non seulement l’hypothèse de Riemann mais également d’autres problèmes mathématiques non résolus. « Les gens vont se plaindre et grincer des dents, mais c’est parce qu’ils rechignent à l’idée qu’un vieil homme puisse avoir apporté une toute nouvelle méthode ».
Lors de sa présentation, le mathématicien anglais a insisté sur la contribution des mathématiciens John von Neumann et Friedrich Hirzebruch, dont les travaux précédents ont servi de base à sa solution. Malgré ces premières critiques et remises en doute, le papier d’Atiyah doit encore être soumis à une évaluation rigoureuse de ses pairs. Pour le moment, et en l’absence de confirmation officielle, il semblerait que l’hypothèse de Riemann ne soit pas prête à rendre ses armes.
L’électron est une particule élémentaire qui, avec les protons et
les neutrons, constitue les atomes. C’est donc l’un des composants
principaux de la matière baryonique. À ce titre, il revêt... [...]