Formulée depuis plus de 100 ans par Albert Einstein, la relativité générale ne cesse d’être mise à l’épreuve au moyen de nombreuses expériences menées depuis plusieurs dizaines d’années. Jusqu’à maintenant, les prédictions d’Einstein ont résisté à tous les tests effectués sur Terre comme dans l’espace. Aujourd’hui, dans le journal Physical Review Letters (1), l’expérience Microscope confirme de nouveau la robustesse de cette théorie.
Le principe d’équivalence : pilier de la physique
D’abord formulé par Galilée dès le 17ème siècle, puis repris par Newton et enfin par Einstein, le principe d’équivalence affirme que deux objets en chute libre tombent à la même vitesse, qu’ils soient de même masse ou de masse différente, à condition que la chute se déroule dans le vide et que les frottements de l’air soient négligés. En d’autres termes, ce principe traduit l’équivalence entre gravité et accélération, c’est-à-dire l’équivalence entre masse gravitationnelle et masse inertielle.
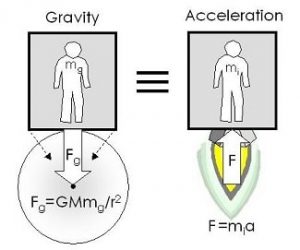
Pour mieux comprendre le principe d’équivalence, il est tout d’abord nécessaire d’établir le bilan des forces impliquées. D’un côté, la gravité que nous connaissons tous. La loi de la gravitation de Newton est formelle à ce propos : plus un objet est massif, plus il est sujet à la gravitation. De l’autre côté, la force d’inertie, décrite par la deuxième loi de Newton : plus un corps est massif, plus la force requise pour modifier son mouvement sera grande.
Maintenant, imaginons deux objets possédant des masses différentes : une pastèque de 1 kg et un stylo de 1 g (rapport de 1000 entre les deux masses). Et, comme Galilée, laissons-les tomber du haut d’une tour. Les deux forces décrites précédemment s’appliquent. La pastèque est gravitationnellement attirée mille fois plus vers le sol que le stylo, tandis que le stylo, lui, subit mille fois moins l’effet de la gravitation. En revanche, la force d’inertie s’oppose mille fois plus à la pastèque qu’au stylo.
Au final, les deux effets s’équilibrent entre les deux objets qui touchent donc le sol simultanément. Néanmoins, une condition stricte doit être respectée pour que ce principe soit correcte. En effet, comme le souligna Newton il y a quelques siècles, les masses gravitationnelle et inertielle doivent être identiques. En d’autres mots, elles doivent être parfaitement équivalentes.
Le principe d’équivalence à l’épreuve de l’expérience
Il y a 500 ans, Galilée aurait laissé tomber une plume et du plomb du haut de la tour de Pise, et se serait ainsi rendu compte que les deux objets, de masses pourtant différentes, touchaient le sol au même moment, réfutant les propos d’Aristote, persuadé que les objets les plus lourds devaient toucher le sol en premier.
Plus tard, Newton formalise le principe d’équivalence en imposant la condition d’équivalence entre masse inertielle et masse gravitationnelle. À la suite de Newton, c’est Albert Einstein qui s’en empare pour en faire un des piliers fondamentaux de sa théorie de la relativité générale. Changeant la notion de « force gravitationnelle » pour l’interpréter en terme de déformation de l’espace-temps par la présence de corps massifs.
Depuis, le principe d’équivalence n’a cessé d’être testé et confirmé. Par exemple, durant la mission spatiale Apollo 15 menée en 1971, l’astronaute et commandant David Scott, alors sur le sol lunaire, lâche un marteau et une plume. Constatant qu’ils touchent bien le sol en même temps, il jubile face à la caméra de son collègue : « Galileo was right ! » (« Galilée avait raison ! »).

À quelques 340 000 km de là, sur Terre, diverses expériences s’astreignent elles aussi à tester le principe d’équivalence. Grâce aux réflecteurs lunaires installés durant les missions américaines Apollo et les missions russes Lunokhod 1 et 2, la distance Terre-Lune peut être fréquemment mesurée via des lasers émis depuis le sol terrestre et réfléchis sur le même axe par lesdits panneaux. En mesurant celle distance, les astrophysiciens peuvent ainsi mesurer la chute libre de la Lune autour de la Terre avec une précision égale à 10-13 fois la gravité terrestre (2).
Parallèlement, des expériences utilisant des pendules de torsion sont menées. Ainsi, en 2012, la collaboration américaine Eöt-Wash a pu vérifier le principe d’équivalence avec une précision de 10-12 g (2). Ces deux expériences ont constitué des avancées significatives dans la mise à l’épreuve du principe d’équivalence (3).
Microscope : tester le principe d’équivalence avec une précision inégalée
Cependant, c’est au satellite Microscope que l’on doit depuis le 4 décembre 2017 les mesures les plus précises jamais réalisées. En effet, les scientifiques sont parvenus à… (suite à la page suivante)


