L’unification de la relativité générale et de la mécanique quantique est un des enjeux primordiaux de la physique moderne. Ces dernières années, de nombreuses théories à gravité quantique ont progressivement émergé, parmi lesquelles la théorie des superformes, la gravitation quantique à boucles ou encore la géométrie non commutative.
Cependant, si les théories sont de plus en plus pointues, la technologie quant à elle ne permet toujours pas d’offrir les cadres expérimentaux nécessaires pour tester celles-ci. Les conditions expérimentales requises pour procéder à ces tests sont extrêmement difficiles à réunir, les effets de la gravité quantique n’apparaissant qu’à des échelles de l’ordre de la longueur de Planck (soit 1.6×10-35 m) et requièrent donc de très hautes énergies.
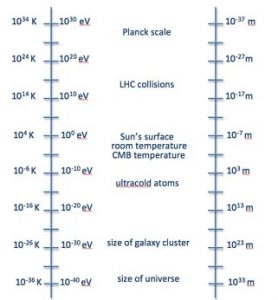
Ces niveaux d’énergie se situent bien au-delà de l’énergie actuellement accessible par les accélérateurs de particules ; par exemple, l’énergie nécessaire pour observer l’échelle de Planck est environ 15 fois plus élevée que celle que le LHC est capable d’atteindre. Pour contourner cette insuffisance technologique, une équipe internationale de physiciens a récemment proposé un protocole permettant de tester la gravité quantique au moyen de notre technologie actuelle.
La non commutativité de l’espace-temps : un paramètre testable de la gravité quantique
Pour le moment, ni les énergies accessibles au sein des accélérateurs de particules, ni les observations astrophysiques ne permettent d’étudier la gravité quantique. Pour autant, les chercheurs ne sont pas piégés dans une voie sans issue. En effet, dans une récente étude publiée dans le journal Nuclear Physics B (1), une équipe internationale de physiciens propose de tester directement un paramètre intrinsèque à toute théorie de la gravité quantique : la non commutativité.
1. La commutativité en mécanique quantique
En mécanique quantique, lorsque l’on décrit un système quantique (comme une particule), l’on utilise une fonction d’onde, c’est-à-dire un outil mathématique contenant les propriétés du système étudié. Cette fonction d’onde contient les différentes caractéristiques du système : énergie, position, spin, vitesse, orientation, etc. Ces caractéristiques sont appelées des « observables » et correspondent donc à des grandeurs physiques mesurables.
Cependant, en mécanique quantique, l’on ne manipule pas directement ces grandeurs ; à la place, on leur assigne ce que l’on appelle des « opérateurs quantiques ». Ces opérateurs sont simplement des objets mathématiques formalisant/représentant les observables. Il y a ainsi l’opérateur position, l’opérateur vitesse, l’opérateur spin… Ce sont donc ces opérateurs qui sont utilisés pour décrire le système.
La relation qu’entretiennent les différents opérateurs entre eux peut être décrite à l’aide d’un paramètre particulier : la commutativité. La commutativité indique s’il est possible de mesurer simultanément deux grandeurs ou non. Ainsi, si deux opérateurs sont commutatifs, les grandeurs qu’ils représentent peuvent être mesurées simultanément. Au contraire, s’ils ne sont pas commutatifs (non commutatifs), alors les deux grandeurs représentées ne peuvent pas être mesurées simultanément.
Mathématiquement, on parle du commutateur entre deux opérateurs. Pour deux opérateurs A et B, le commutateur s’écrit [A,B] = AB-BA. L’essentiel à retenir ici est que si le commutateur est nul, alors les deux opérateurs sont commutatifs. À l’inverse, si le commutateur est non-nul, alors les deux opérateurs sont non commutatifs. Deux opérateurs non commutatifs sont appelées des « observables complémenaires » ou des « variables conjuguées ».
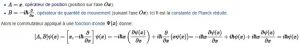
Un exemple célèbre d’opérateurs non commutatifs est donné par le principe d’indétermination d’Heisenberg. Ce principe énonce que, pour une particule, il est impossible de mesurer simultanément avec une précision identique sa position et sa quantité de mouvement. En d’autres mots, l’opérateur position « x » et l’opérateur quantité de mouvement « p » d’une particule sont non commutatifs.
2. La non commutativité dans les théories à gravité quantique
La plupart des théories à gravité quantique actuelles sont axées sur la non commutativité (2) et font de celle-ci un paramètre essentiel dans la description de l’espace-temps (3, 4, 5). Par exemple, en théorie des cordes, la plus petite longueur d’espace mesurable correspond à la longueur d’une corde. En dessous de cette longueur, l’espace-temps n’existe plus. Cela est dû à la non commutativité de certains opérateurs décrivant l’espace-temps (6).
Dans les théories à gravité quantique, l’espace-temps possède donc une structure non commutative ; l’on parle également de géométrie non commutative. Une telle structure implique des conséquences directes à l’échelle cosmologique. Ainsi, dans les théories à gravité quantique, la non commutativité permet de faire disparaître les singularités gravitationnelles, de préciser la topologie de l’espace-temps durant l’ère de Planck ou encore de mieux comprendre la véritable nature des trous noirs.
Et selon les auteurs de l’étude, la non commutativité de l’espace-temps est un paramètre directement testable au moyen de notre technologie actuelle. Puisque la non commutativité est un élément clé des théories à gravité quantique, confirmer physiquement sa présence permettrait de conforter solidement les différentes théories actuelles sans avoir besoin d’atteindre les énergies nécessaires à la mise en évidence des effets quantiques de la gravité.
Une expérience accessible pour tester la non commutativité
La volonté d’étudier les effets quantiques émergeant à l’échelle de Planck n’est pas nouvelle. En effet, plusieurs études ont déjà proposé des protocoles expérimentaux utilisant des technologies optiques disponibles dans le but d’observer certains phénomènes quantiques (7, 8). En s’appuyant sur ces études, les auteurs proposent d’observer la structure non commutative de l’espace-temps via un nouveau dispositif optique.
À ce sujet, Mir Fraizal (University of Lethbridge, Canada) explique que « nous nous attendons à ce que la géométrie de l’espace-temps soit une structure émergente telle que décrite mathématiquement par les théories à gravité quantique. La plupart des théories à gravité quantique suggèrent que cette structure contenant la géométrie de l’espace-temps peut être représentée par une géométrie non commutative. Ainsi, nous proposons une nouvelle façon de tester cette idée en utilisant un dispositif opto-mécanique ».
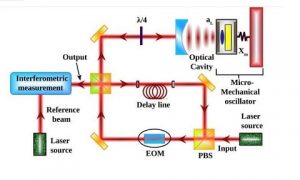
Pour ce faire, les chercheurs proposent d’utiliser un oscillateur quantique micromécanique placé dans une cavité optique. Un tel oscillateur est caractérisé par certains opérateurs quantiques commutatifs ; on parle de « relations commutatives » entre les opérateurs. À l’intérieur de la cavité optique, l’oscillateur quantique micromécanique est soumis à une pression de radiation continue. En d’autres termes, un flux continu de photons est émis en sa direction, l’oscillateur interagissant avec chacun des photons.
Toute modification/déformation des relations commutatives de l’oscillateur, indiquant la présence concrète d’une non commutativité de la structure de l’espace-temps, induirait une déviation mesurable de la phase optique du faisceau lumineux (source des photons) couplée à l’oscillateur. En d’autres termes, une modification quantique du faisceau de lumière impliquerait la présence d’une non commutativité de la géométrie de l’espace-temps.
Un tel changement de phase dans le rayon lumineux serait bien sûr infime. Dans le but de pouvoir détecter et mesurer un tel changement, les physiciens utilisent un interféromètre. En effet, un interféromètre est un appareil permettant de mesurer d’infimes variations au sein d’un système de taille variable.
Le dispositif opto-mécanique est tout à fait viable et opérationnel avec les technologies actuelles. Ainsi, l’utilisation combinée d’un oscillateur micromécanique couplé à une source lumineuse et à un interféromètre permettrait de mettre en lumière la nature non commutative de l’espace-temps, et donc de tester directement la gravité quantique. Mieux encore, les auteurs précisent qu’en améliorant la sensibilité de la cavité optique, il serait possible d’observer ces effets à l’échelle de Planck.
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]