La théorie des nombres est une branche des mathématiques étudiant les propriétés des nombres entiers. Elle est un domaine actif de recherche en mathématiques fondamentales, car elle se situe à l’interconnexion de toutes les autres disciplines. En analysant précisément une fonction analytique particulière de la théorie, la forme modulaire, un duo de chercheurs a montré que dans certains cas, cette fonction pouvait être décrite par l’intermédiaire d’observables quantiques dans la théorie des supercordes. Un résultat qui pourrait aider à conforter certaines propriétés de cette théorie.
La collaboration d’un mathématicien et d’un physicien a montré que les formes modulaires associées aux courbes elliptiques avec des multiplications complexes sont exprimées en termes d’observables dans la théorie des supercordes. L’étude a été publiée dans la revue Communications in Mathematical Physics. Le concept de nombres peut être étendu à partir d’entiers et de nombres rationnels pour inclure tous les nombres réels et les nombres complexes.
Mais il est également possible d’étendre progressivement le concept, en ajoutant peu à peu les racines des polynômes avec des coefficients à nombre rationnels (comme la racine carrée de 2 et la racine carrée de 3). Cette classe spéciale de nombres complexes est appelée « nombres ». Les détails précis sur la manière dont le concept de nombres peut être étendu ont été considérés comme l’un des thèmes importants de la théorie des nombres.
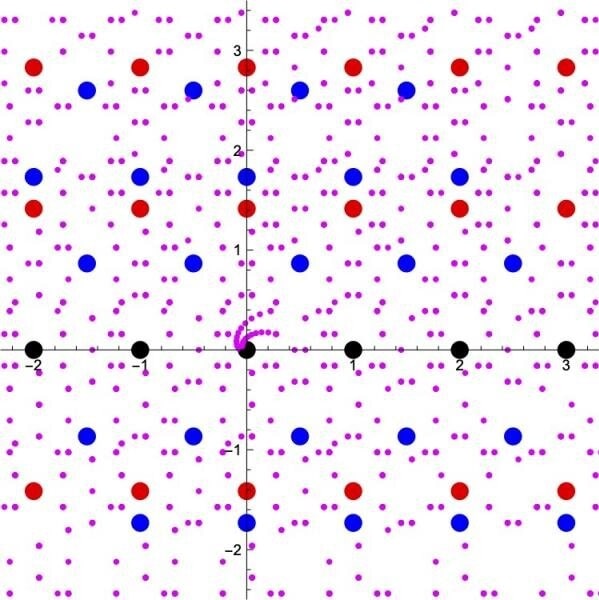
L’invariance de la transformée de Mellin inverse de la fonction L
Depuis plusieurs décennies, les chercheurs tentent de résoudre et de comprendre ce problème. On pourrait spécifier un objet géométrique par des équations en utilisant d’abord les « nombres », puis considérer l’ensemble des points de l’objet géométrique dont les valeurs sont les « nombres ». Au fur et à mesure que le concept de nombres s’élargit et que l’ensemble des « nombres » en fait de même, de plus en plus de points dans l’objet géométrique sont comptés.
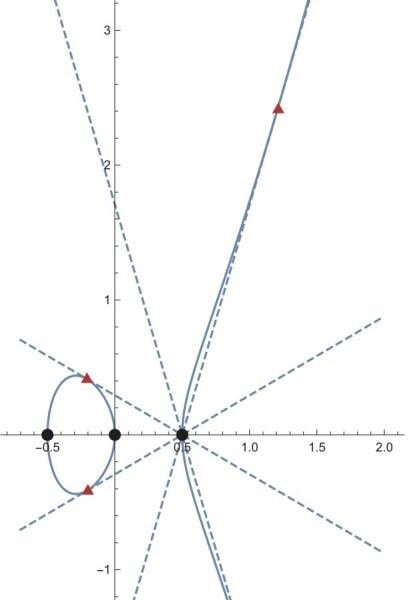
L’idée est que la façon dont le nombre de points dans l’objet géométrique augmente éclairera la façon dont l’ensemble des « nombres » se développe. En outre, ces informations sur le taux de croissance du nombre de points dans l’objet géométrique sont regroupées dans une fonction appelée la transformation de Mellin inverse de la fonction L, qui est une fonction contenant les informations sur la vitesse à laquelle le nombre de points dans un objet géométrique grandit à mesure que le concept de nombres est étendu.
Cette fonction devait être une forme modulaire, une fonction qui reste invariante sous certaines opérations. Cette conjecture est connue sous le nom de conjecture de Langlands.
Taizan Watari et Satoshi Kondo, de l’Institut Kavli pour la physique et les mathématiques de l’univers (Kavli IPMU), se sont demandés pourquoi ces fonctions sont invariantes dans certaines opérations.
Sur le même sujet : Une IA de Facebook est maintenant capable de résoudre des problèmes mathématiques de niveau universitaire en quelques secondes
Des formes modulaires descriptibles en termes d’observables dans la théorie des supercordes
En théorie des supercordes, il est connu qu’une classe d’observables (a) est invariante sous les opérations (x) déjà évoquées. L’invariance sous les opérations est une propriété indispensable dans la construction théorique de la théorie des supercordes. Ainsi, les chercheurs ont montré que les transformées de Mellin inverses des fonctions L des objets géométriques (b) sont exprimées en termes de la classe d’observables (a) dans la théorie des supercordes, avec ces objets géométriques définis comme les espaces cibles.
En conséquence, il s’ensuit que les fonctions contenant les informations sur la façon dont le concept de nombres est étendu, les transformées de Mellin inverses (b), devraient être invariantes sous certaines opérations, qui devraient être des formes modulaires (x) pour des raisons du point de vue de la théorie des supercordes.
Il est à noter que le résultat ci-dessus n’est obtenu que pour la classe d’objets géométriques appelés courbes elliptiques à multiplications complexes. La question reste ouverte de savoir si les fonctions d’une classe plus générale d’objets géométriques (b) sont exprimées en termes d’observables dans la théorie des supercordes (a).

