Hypothèse prééminente et déterminante en physique théorique, le principe holographique est actuellement utilisé dans un grand nombre de théories, il constitue notamment un des socles de base des théories à gravité quantique. Pilier principal de la physique des cordes, il permet aujourd’hui de résoudre le paradoxe de l’information, d’offrir un cadre élégant à la gravité quantique ou encore de simplifier des calculs en physique de la matière condensée.
I. Le paradoxe de l’information
En 1974, le physicien Stephen Hawking démontre que les trous noirs subissent un phénomène d’évaporation et que l’information qu’ils contiennent, celle de la matière absorbée au cours du temps, est définitivement perdue lors de cette évaporation. Cependant, selon la mécanique quantique, l’information ne peut jamais être détruite, elle fait l’objet d’un principe fondamental de conservation. Cette potentielle perte d’information dans les trous noirs, contraire aux postulats de la mécanique quantique, adopte très vite le nom de « paradoxe de l’information ».
II. L’entropie des trous noirs et la solution au paradoxe de l’information
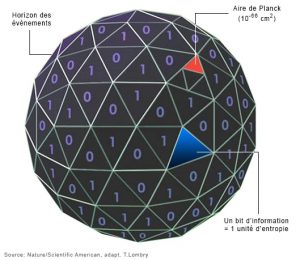
Dans le même temps, le physicien Jacob Bekenstein montre (1) qu’il existe une limite maximale à l’entropie, c’est à dire la quantité d’information, qu’un volume d’espace peut contenir. La matière et l’énergie sont entièrement définies par leur information, et cette information se décompose en bits (0 et 1). Bekenstein démontre que dans une région donnée d’espace, il existe une quantité maximale de bits pouvant décrire la masse et l’énergie contenues dans cette région. Mais surtout, il démontre que cette quantité maximale d’information/entropie est proportionnelle à l’aire de la région considérée. Par extension, il montre que l’entropie d’un trou noir est proportionnelle à l’aire de son horizon des événements et donc à sa surface.
En 1993, le physicien Gerard ‘t Hooft s’appuie sur les travaux de Bekenstein et montre que la surface totale d’un trou noir peut être décomposée en unités fondamentales : les aires de Planck mesurant 10-66 cm2. En utilisant les calculs de Hawking, il indique que 4 aires de Planck définissent 1 nat (unité d’entropie/information). À partir de ceci, il propose la solution suivante au paradoxe de l’information (2) : lorsque de la matière ou de l’énergie tombe dans un trou noir, son information est encodée sur la surface bidimensionnelle du trou noir, c’est à dire dans le réseau formé par les aires de Planck. Cette information est donc restituée lors de l’évaporation du trou noir. Ainsi, si l’on veut savoir ce que « contient » le trou noir, il suffit de lire l’information encodée à sa surface.
III. Le principe holographique
Sur la base de tous ces travaux, le physicien Leonard Susskind publie, en 1995, « World as a hologram » (3), dans lequel il donne une explication plus globale de ce phénomène : tout ce qui est contenu dans un volume d’espace peut être décrit par l’information contenue à la surface de ce volume. Puisque la quantité maximale d’information d’un volume ne peut être supérieure à celle stockée à la surface de celui-ci, alors l’information emmagasinée à la surface d’un volume est amplement suffisante pour le décrire. Ce principe adopte ainsi le nom de « principe holographique », en référence à l’image 3D encodée dans un hologramme (holographie).
Dans sa publication, Susskind postule que le volume total de l’univers dans lequel nous évoluons n’est en réalité qu’un hologramme dont la source est l’information encodée à la surface de ce dernier. Cela permettrait ainsi la projection d’un hologramme isomorphe (en tout point identique) composant le volume occupé par notre univers.
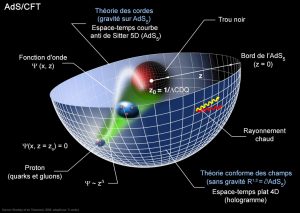
En 1997, le physicien Juan Maldacena propose une description exhaustive du principe holographique dans une théorie appelée « correspondance AdS/CFT » (4). Dans ce cadre théorique, Maldacena montre qu’une théorie des cordes contenue dans un espace anti de Sitter à 5 dimensions (modèle d’univers particulier composé uniquement d’une constante cosmologique négative), noté AdS5, est équivalente à une théorie conforme des champs (théorie quantique décrivant les interactions élémentaires) contenue sur le bord à 4 dimension de cet espace (ce bord étant semblable à notre espace-temps).
Des calculs trop complexes à réaliser dans le cadre de la théorie conforme des champs seraient alors réalisables plus facilement dans le cadre de la théorie des cordes en se servant des équivalences de la correspondance AdS/CFT. Par des transformations adéquates, les événements physiques émergeant dans notre univers à 4 dimensions (le bord de l’espace AdS5) peuvent ainsi être décrits, via la principe holographique, dans l’univers anti de Sitter. Bien que l’univers anti de Sitter ne soit absolument pas un univers réaliste, la correspondance AdS/CFT offre néanmoins de puissants outils théoriques à l’exploitation du principe holographique.
IV. Le principe holographique et le rayonnement de Hawking
Puis plus récemment, en 2015, Hawking tient compte des avancées en théorie des supercordes et se base sur les travaux de Susskind et Maldacena pour présenter une nouvelle hypothèse résolvant son propre paradoxe de l’information. Il explique que les particules absorbées par un trou noir modifient la géométrie de l’horizon des événements de ce dernier en réalisant une « supertranslation » (notion mathématique complexe décrivant la conservation de certaines symétries, notamment celle de l’information). L’information des particules absorbées est donc encodée sous forme de supertranslations qui agissent comme des hologrammes sur l’horizon des événements et forment une empreinte quantique des particules disparues. Par la suite, l’horizon des événements étant le siège de fluctuations quantiques, l’information est réémise (et donc restituée), par ces fluctuations composant le rayonnement de Hawking.


 Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]
Un trou noir
est un objet compact au champ gravitationnel si intense qu'aucune
matière ni aucun rayonnement ne peut s'en échapper. Puisque ces
astres n'émettent aucune lumière, ils ne peuvent être... [...]
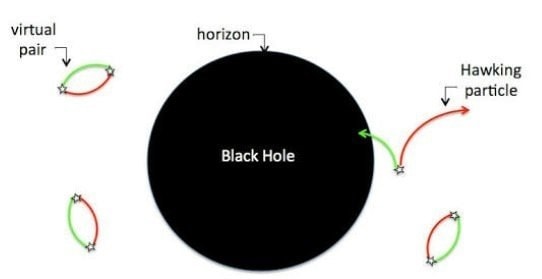 Selon la théorie développée par Stephen Hawking, les trous noirs
s'évaporent et ne seraient pas "totalement noirs". Ils seraient
légèrement luisants et constamment en train d’émettre des
particules par intensité faible depuis leur surface. Il s’agit du
rayonnement de Hawking [...].
Selon la théorie développée par Stephen Hawking, les trous noirs
s'évaporent et ne seraient pas "totalement noirs". Ils seraient
légèrement luisants et constamment en train d’émettre des
particules par intensité faible depuis leur surface. Il s’agit du
rayonnement de Hawking [...].